はじめに

本番で解けなかった問題を解いてみます。今回は問１です。この問題で問われていることは

です。似たような問題ないかなぁと調べてみるとなんと、アクチュアリーの昭和39年数学1の問３にほぼ同じような問題があったので、これを見つつ今回の問題を解いてみることにしました。

問題を解く

以下、

を代入すると記述1〜記述4の解となります。

ポアソン分布 $P(X = k ; {\lambda}) = exp(-{\lambda}) \Big( \frac{ {\lambda}^k }{k!} \Big)$ は、

です。

$P(X = k ; \lambda_1), P(Y = k ; {\lambda}_2)$ の時、 $P(X + Y = Z )$ が従う分布を求めます。

(はてなのmathjax記法がエラるので画像にて。。)

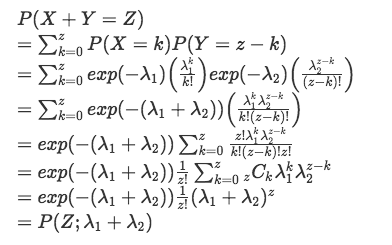
となるので、

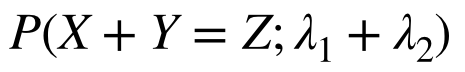
が和の分布となる(ポアソン分布の再生性が確認できた)。よって、和の分布は

となる。

求めるのは、

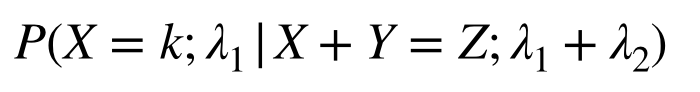
という確率分布である。計算すると、

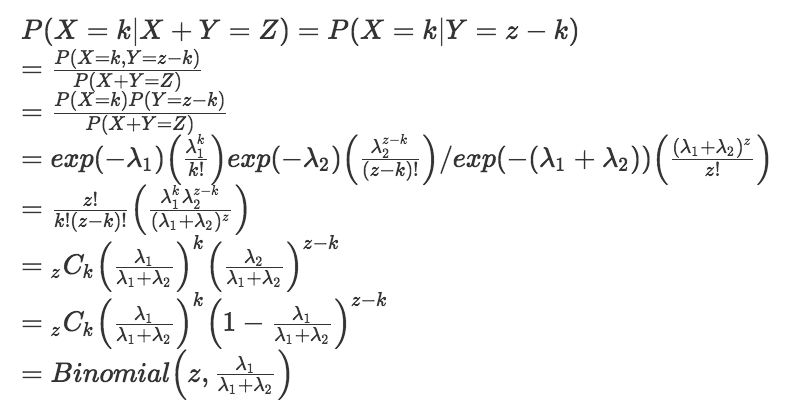
となるので、この条件付き確率分布は二項分布となる。

したがって、平均値は

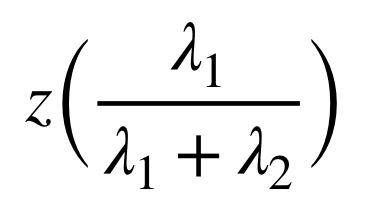
となる。