統計学実践ワークブックのp.281あたりです。

補助公式

以下が成り立つため、

$\displaystyle t\exp(-t^2/2) = \left(-\exp(-t^2/2)\right)'$

標準正規分布の確率密度関数 $\varphi(t)$ を用いても以下が成り立つ

$\displaystyle t\varphi(t)= t\frac{1}{\sqrt{2\pi}}\exp(-t^2/2) \\ \displaystyle = (-\frac{1}{\sqrt{2\pi}}\exp(-t^2/2))'\\ \displaystyle = (-\varphi(t))'$

問題

確率変数 $Z$ の確率密度関数が

$\displaystyle f(z) = \begin{cases} \displaystyle \frac{1}{\Phi(a)} \varphi(z) \quad (z \lt a) \\ \displaystyle 0 \quad \text{otherwise } \displaystyle \end{cases}$

と与えられる時の期待値・分散を求めよう。

期待値

$\displaystyle E[ Z | Z \lt a]$ は、

$\displaystyle E[Z|Z \lt a] = \\ \displaystyle \int_{-\infty}^{a} \frac{1}{\Phi(a)} t \varphi(t)dt\\ \displaystyle = \int_{-\infty}^{a} \frac{1}{\Phi(a)}(-\varphi(t))'dt\\ \displaystyle = \left[-\frac{\varphi(t)}{\Phi(a)}\right]_{\infty}^{a} \\ \displaystyle = \frac{\varphi(\infty)-\varphi(a)}{\Phi(a)} \\ \displaystyle = -\frac{\varphi(a)}{\Phi(a)}$

となる。

分散

$\displaystyle V[ Z|Z \lt a ] = E[ Z^2|Z \lt a ] - \left(E[ Z|Z \lt a ]\right)^2$

より、 $E[ Z^2|Z \lt a]$ を計算すると、

$\displaystyle E[Z^2|Z \lt a] = ∫_{-\infty}^{a} \frac{1}{\Phi(a)} z^2 \varphi(z)dz\\ \displaystyle = ∫_{-\infty}^{a} \frac{1}{\Phi(a)} z \cdot \left(z\varphi(z)\right)dz\\ \displaystyle = ∫_{-\infty}^{a} \frac{1}{\Phi(a)} z \cdot \left(-\varphi(z)\right)' dz\\ \displaystyle = \Bigl[ -z\varphi(z) \Bigr]_{-\infty}^{a}/\Phi(a) + ∫_{-\infty}^{a} \varphi(z) /\Phi(a)dz \\ \displaystyle = -\frac{a\varphi(a)}{\Phi(a)} + 1$

となることから、

$\displaystyle V[ Z|Z \lt a ] = -\frac{a\varphi(a)}{\Phi(a)} + 1 - \left( \frac{\varphi(a)}{\Phi(a)} \right)^2$

となる。

ここで

$\displaystyle \lim_{z\to -\infty} z\varphi(z) = \lim_{z\to -\infty} z \frac{1}{\sqrt{2 \pi}}\exp(-z^2/2)\\ \displaystyle \propto \lim_{z\to -\infty} \frac{z}{\exp(z^2/2)}\\ \displaystyle = \lim_{z\to -\infty} \frac{(z)'}{(\exp(z^2/2))'} \\ \displaystyle = \lim_{z\to -\infty} \frac{1}{z\exp(z^2/2)} = \frac{1}{-\infty \times \infty} = \frac{1}{-\infty} = 0$

を用いた(ロピタルの定理)

2023-02-12

統計学実践ワークブック第3章：分布の特性値〜繰り返し期待値の法則および繰り返し分散の法則〜

統計学実践ワークブック

統計学実践ワークブックのp.17です。ふわっと証明します。

繰り返し期待値の法則

$\displaystyle E[ Y ] = E[ E[ Y | X ] ]$

証明

$\displaystyle E[ E[ Y|X ] = E^X [ E^{Y|X} [ Y|X ] ] \\ \displaystyle = E^X[ \sum_y y P(Y=y | X= x) ] \\ \displaystyle = \sum_x \sum_y y P(Y=y | X= x) P(X=x) \\ \displaystyle = \sum_x \sum_y y P(Y=y , X=x ) \\ \displaystyle = \sum_y y \sum_x P(Y=y , X=x ) \\ \displaystyle = \sum_y y P(Y=y) \\ \displaystyle = E[ Y ] \\$

繰り返し分散の法則

$\displaystyle V[ Y ] = E[ V[ X|Y ] ] + V[ E[ X|Y ]]$

証明

$\displaystyle V\left[ Y \right] = E\left[ Y^2 \right] - \left(E\left[ Y \right]\right)^2 \\ \displaystyle = E\left[ E\left[ Y^2 | X \right] \right] - \left(E\left[ E \left[ Y| X \right] \right] \right) ^2 \\ \displaystyle = E\left[ V\left[ Y|X \right] + \left(E\left[ Y | X \right]\right)^2 \right] - \left(E\left[ E \left[ Y| X \right] \right] \right) ^2 \\ \displaystyle = E\left[ V\left[ Y|X \right] \right] + E\left[ \left(E\left[ Y | X \right]\right)^2 \right] - \left(E\left[ E \left[ Y| X \right] \right] \right) ^2 \\ \displaystyle = E\left[ V\left[ Y|X \right] \right] + V\left[ E\left[ Y | X \right] \right]$

参考

en.wikipedia.org
en.wikipedia.org

2023-02-12

統計検定準１級(CBT)に合格したので勉強法やら書籍やらを書いておきます。

統計検定統計学実践ワークブック陳述

ギリギリですが合格しました。#統計検定準1級 pic.twitter.com/RVCSsQhUpB
— Satoaki Noguchi (@axjack_) 2023年2月11日

感想
受験に臨むにあたって(勉強以外編)
成績
勉強法
書籍
webサイト
youtube

感想

CBTってどんな感じなのかな？とあくまで試験の慣らし運転ぐらいの気持ちで受験に臨んだのですが、棚からぼたもち的な流れで合格していました。「合格」の文字が出た時は思わず「え？」と変な声が出ました(笑

受験に臨むにあたって(勉強以外編)

荷物をロッカーに入れます
- 荷物が多いと入らないかもしれないので注意です。
教室内は電卓だけ持ち込み可でした
- 時計もスマホも参考書も持ち込み不可だったので、受験会場に入るまでに予習は済ませておきましょう。
Odyssey ID、パスワードを暗記しておく必要がある
- 荷物・スマホはロッカーにあるので、IDパスワードを覚えておく必要があります。変に焦らぬように事前にログインできるか確認しておきましょう。
時計がなくても試験の残り時間は画面の左下に表示されます
電卓は必須です。おそらく使います。
計算"用紙"ではなくてラミネート加工されたツルツル紙に水性ペン？的なもので計算します

成績

評価得点：65点
1. 確率と確率分布：60%
2. 統計的推測：33%
3. 多変量解析法：76%
4. 種々の応用：85%

配点ウェイトどうなってるんだ・・・？

勉強法

統計学実践ワークブックを精読、行間を埋めるが中心でした。過去問はほとんど解いていないです。A4レポート用紙に式変形をひたすら書いて、はてなブログに勉強したことのまとめを書いてスマホにまとめを書いて、の繰り返しです。

準1級の勉強を通じて、なぜかLaTeX力がついた気がします。

書籍

統計検定特化型の書籍

統計学実践ワークブック
- 準1級CBTは「統計学実践ワークブック検定」といっても過言ではないかもです。それぐらい内容が網羅されていると思います。
- なのでこれさえ理解すれば大丈夫です。ただ、私のようなただの凡人にはワークブックだけで内容が分かるようなつくりにはなっていないので、他の書籍/webサイトで知識を補う必要があります。
統計検定準1級公式問題集
- 購入しましたがほとんど解いていないです
日本統計学会公式認定　統計検定１級対応　「統計学」
- １級用なので準1級向けではない気がしますが、ワークブックでよくわからない式変形が出てきたときに役に立ちました

統計学全般の書籍

数式変形のお供に。

統計学入門(東京大学出版会)
- ２級受けた人なら手元にあるはず？たまに参考にします
自然科学の統計学(東京大学出版会)
- ワークブックでよくわからない式変形が出てきたときに役に立ちました
久保川達也現代数理統計学の基礎
- ワークブックでよくわからない式変形が出てきたときに役に立ちました

買ったけど役に立ったか微妙なライン

本格的に学ぶには早すぎたかも？という意味で役に立ったか微妙でした。ただ、買って損はしないです。

ドブソン一般化線形モデル入門
Rによる統計的学習入門
はじめてのパターン認識
ベイズ推論による機械学習入門
RとPythonで学ぶ［実践的］データサイエンス＆機械学習

webサイト

youtube

Yuya Kawaguchi - YouTube

2023-02-02

確率変数の変数変換：一様分布に従う2 つの確率変数の和

統計勉強

理論編
例：一様分布に従う2 つの確率変数の和

理論編

確率変数 $X,Y$ の同時確率密度関数(joint pdf)を $f_{X,Y}(x,y)$ とする。この時、 $X,Y$ を

$\displaystyle \begin{bmatrix} Z \\ W \end{bmatrix} = \begin{bmatrix} u(X,Y)\\ v(X,Y) \end{bmatrix}$

と変数変換(change of variables)することを考える。ただし、 $u,v$ には逆変換が存在しそれを、

$\displaystyle \begin{bmatrix} X \\ Y \end{bmatrix} = \begin{bmatrix} s(Z,W)\\ t(Z,W) \end{bmatrix}$

と表す。ここでヤコビアン $J(X,Y)$ を

$\displaystyle J(X,Y) = \det \left( \begin{bmatrix} \frac{\partial Z}{ \partial X} & \frac{\partial Z}{ \partial Y} \\ \frac{\partial W}{ \partial X} & \frac{\partial W}{\partial Y} \end{bmatrix} \right)$

とすると、変数変換後の同時確率密度関数 $f_{Z,W}(z,w)$ は、

$\displaystyle f_{Z,W}(z,w) = f_{X,Y} ( x, y ) / | J(X,Y) | \\ = f_{X,Y}( s(z,w), t(z,w) ) / | J(X,Y)|$

で表される(ここで $|\cdot|$ は絶対値を表す)。

また、確率変数 $X,Y$ が独立でそれぞれの確率密度関数が $f_X(x), f_Y(y)$ で与えられていれば、

$\displaystyle f_{Z,W}(z,w) = f_{X,Y} ( x, y ) / | J(X,Y) | \\ = f_{X,Y}( s(z,w), t(z,w) ) / | J(X,Y)| \\ = f_X(s(z,w)) f_Y( t(z,w) )/ | J(X,Y) |$

となる。

さらに、同時確率密度関数 $f_{Z,W}(z,w)$ を $w$ で積分消去(integrate out, marginal, collapse)することで確率変数 $Z$ の周辺確率密度関数(marginal pdf)を求めることができる。すなわち、

$\displaystyle f_Z(z) = ∫_{-\infty}^{\infty} f_{Z,W}(z,w) dw = ∫_{-\infty}^{\infty} \frac{1}{ |J(X,Y)| }f_{X,Y}( s(z,w), t(z,w) )dw$

となる。

例：一様分布に従う2 つの確率変数の和

確率変数 $X,Y$ はそれぞれ独立に一様分布 $\text{Unif}(0,1)$ に従うとする。確率密度関数 $f_X(x), f_Y(y)$ は

$\displaystyle f(t) = \begin{cases} 1 \quad \text{if} \quad 0 \lt t \lt 1 \\ 0 \quad \text{otherwise} \end{cases}$

を用いて、 $f_X(x) = f(x)$ および $f_Y(y) = f(y)$ で与えられる。

確率変数の変換

確率変数 $Z,W$ を $Z = X+Y, W = Y$ と変換する。このとき $X = Z - W, Y = W$ である。

またヤコビアン $J(X,Y)$ は、
$J(X,Y) = det \begin{pmatrix} \frac{∂Z}{∂X} & \frac{∂Z}{∂Y} \\ \frac{∂W}{∂X} & \frac{∂W}{∂Y} \end{pmatrix} = det \begin{pmatrix} \frac{∂(X+Y)}{∂X} & \frac{∂(X+Y)}{∂Y} \\ \frac{∂Y}{∂X} & \frac{∂Y}{∂Y} \end{pmatrix} \\ = det \begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix} = det (1) = 1$ である。

同時確率密度関数

独立なので $f_{X,Y}(x,y) = f_X(x) f_Y(y) = f(x)f(y)$ である従って、 $f_{Z,W}(z,w)$ は

$f_{Z,W}(z,w) = f_{X,Y}(x,y)/|J(X,Y)| = f(x)f(y)/1 = f(x)f(y) = f(z-w)f(w)$

となる。

確率変数のとりうる領域

与えられた情報からまとめると、

$0 \lt X \lt 1$
$0 \lt Y \lt 1$
$X = Z - W$ より $0 \lt Z-W \lt 1$
$Y = W$ より $0 \lt W \lt 1$

なる不等式を得る。従って、 $z,w$ に関する領域を書くと下記となる。

この図をw軸の視点で見ると、

$0 \lt z \lt 1$ のとき $0 \lt w \lt z$
$1 \lt z \lt 2$ のとき $z-1 \lt w \lt 1$

となる。

領域の書き方補足

周辺確率密度関数にて $w$ で積分消去することを念頭に置いて、 $z$ を固定したときの $w$ を変数とする領域、をイメージすると良い。
$0 \lt z-w \lt 1$ は $z-w = k$ とし、 $z = k + w$ の直線を $0 \lt k \lt 1$ で動かすことで得られる。
w軸と平行な線分が、zに依存しつつ線分の長さを変えながら動いた結果が水色の領域、というイメージ。

周辺確率密度関数

和の分布なので $Z$ の確率密度関数を求めれば良い。従って $f_{Z,W}(z,w)$ を $w$ で積分消去する。ここで、積分範囲を明示せずに書くと、

$\displaystyle f_Z(z) = ∫ f_{Z,W}(z,w)dw = ∫f(z - w)f(w)dw = ∫f(z-w)dw$
となる。
積分範囲は $z$ に依存しているので、２通りに分けて書く。

$0 \lt z \lt 1$ のとき $0 \lt w \lt z$

$\displaystyle f_Z(z) = ∫_{0}^{z} f(z-w) dw = ∫_{0}^{z} 1 dw = \Bigl [ w \Bigr]_0^z = z-0 = z.$

$1 \lt z \lt 2$ のとき $z-1 \lt w \lt 1$

$\displaystyle f_Z(z) = ∫_{z-1}^{1} f(z-w) dw = ∫_{z-1}^{1} 1 dw = \Bigl [ w \Bigr]_{z-1}^1 = 1 - (z-1) = 2 - z .$

となる。まとめると、

$\displaystyle f_Z(z) = \begin{cases} z \quad \text{if} \quad 0 \lt z \lt 1 \\ 2 - z \quad \text{if} \quad 1 \lt z \lt 2 \end{cases}$
となる。

参考

math.stackexchange.com

2022-10-01

列空間と左零空間は直交する

線形代数

準備

行列Aを
- $A \in \mathbb{R}^{m \times n}$
Aの列空間を
- $C(A) = \{ Ax \mid x \in \mathbb{R}^{n} \} \subset \mathbb{R}^m$
Aの左零空間を
- $N(A') = \{ x \mid A'x = \vec{0} \} \subset \mathbb{R}^m$

とする。この時、C(A)の任意のベクトルとN(A')の任意のベクトルは直交する。

確認

x ∈ C(A), y ∈ N(A')を任意に取る。ベクトルが直交することを示すには内積が0となることを確認すれば良い。なお、小文字のoを零ベクトルとする。

すると、

x'y = (Aw)'y = w'A'y = w'(A'y) = w'o = 0
y'x = y'(Aw) = (y'A)w = (A'y)'w = o'w = 0

となってy'x = x'y = 0が示せた。

したがって、C(A)の任意のベクトルとN(A')の任意のベクトルは直交する。
□

2022-09-15

ecdf関数とstepfun関数

R プログラミング

ecdf関数は経験累積分布関数を返す関数
stepfun関数はステップ関数・区分関数・単関数(?)を返す関数

d <- c(1:10)
Fn <- ecdf(d)
plot(Fn)

knots(Fn)

Gn <- stepfun(d,c(1,3,2,5,4,7,3,3,4,2,1))

plot(Gn)

2022-09-12

統計学実践ワークブック：第13章ノンパラメトリック法

R プログラミング統計学実践ワークブック

Rで実装してみた。

p100~: ウィルコクソンの順位和検定
p102~: 並び替え検定
p102~: ウィルコクソンの符号付き順位和

gist.github.com

2022-09-11

R勉強会　第5回　アウトプット用課題の問5,6を解く

プログラミング R

qiita.com

QittaのR言語記事を散策していたら@roadricefieldさんの面白い記事があったので、自分でも解いてみることにしました。

問5
問6
- 関数
- 実行

問5

極値を求める関数を作成する問題。

関数

extremum_detector <- function(d, k){
  # 補助関数
  f <- function(a,k){
    judge <- rep(c(1,-1),each=(k-1)/2)
    sdf <- sign(diff(a))
    all(sdf == judge)||all(sdf == rev(judge))
  }

  if(k < 3 || k %% 2 == 0) stop()
  # extremum pointを返す
  which(apply(embed(d,k),MARGIN=1,f,k)) + (k-1)/2
}

実行

５点近傍での極値

dev.off()
data <- c(1, 2, 3, 2, 1, 0, 1, 0, -1, 2, 3, 2, 1)
extremum.points <- extremum_detector(data, 5)
plot(data, type="b")
points(extremum.points, data[extremum.points],col = "red",pch=16)

３点近傍での極値

dev.off()
data <- c(1, 2, 3, 2, 1, 0, 1, 0, -1, 2, 3, 2, 1)
extremum.points <- extremum_detector(data, 3)
plot(data, type="b")
points(extremum.points, data[extremum.points],col = "red",pch=16)

embed関数なるものを使うと、系列を左から $d$ 個ずつスライドして取り出すことができて便利(ただし順番が逆になる点のみ注意)

使用例

> letters[1:12]
 [1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l"

> embed(letters[1:12],4)
      [,1] [,2] [,3] [,4]
 [1,] "d"  "c"  "b"  "a" 
 [2,] "e"  "d"  "c"  "b" 
 [3,] "f"  "e"  "d"  "c" 
 [4,] "g"  "f"  "e"  "d" 
 [5,] "h"  "g"  "f"  "e" 
 [6,] "i"  "h"  "g"  "f" 
 [7,] "j"  "i"  "h"  "g" 
 [8,] "k"  "j"  "i"  "h" 
 [9,] "l"  "k"  "j"  "i"

問6

k-meansクラスタリングを実装する。

関数

my_kmeans <- function(x = x_sample, y = y_sample, k = 3){
  # # 初期クラスタを選択
  # cent_ind <- sample(seq_along(x), k, replace = FALSE)
  # # 初期セントロイドたち
  # cent     <- cbind(x[cent_ind], y[cent_ind])
  # cent     <- cbind(c(91,57,41),c(26,61,14))

    cent     <- sample( (min(x,y)):(max(x,y)), k * 2, replace = FALSE) |> matrix(nrow = k)
  i <- 0
  while(1){
    # セントロイドからの距離が最小となるような所属を求める
    M <- rbind(cent, cbind(x,y)) |> dist() |> as.matrix()
    belong <- M[-(1:k),1:k] |> apply(MARGIN = 1, which.min)

    # 新しいセントロイド
    cent_new <- cbind(tapply(x, belong,  mean), tapply(y, belong,  mean))
    i <- i+1
    cost <- sum((cent_new - cent)^2)
    print(paste("iter = ",i,", cost = ", cost))
    
    # costが1より小さかったらループ終了
    if ( cost < 1 ) break

    # セントロイドの更新
    cent <- cent_new
  }
  
  # 所属を返す
  return( belong |> as.numeric() )
}

実行

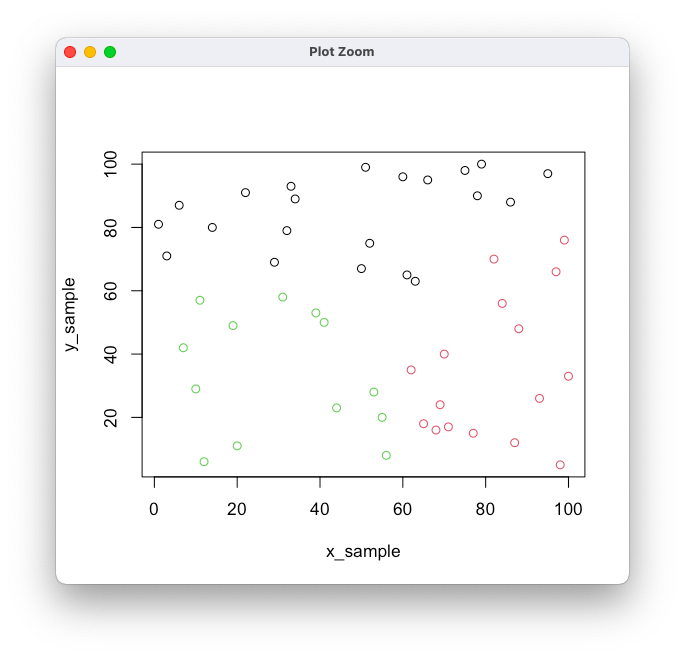
dev.off();
set.seed(2022)
x_sample <- sample(1:100, 50, replace = FALSE)
y_sample <- sample(1:100, 50, replace = FALSE)
clst <- my_kmeans(x_sample, y_sample, k = 3)
plot(x_sample, y_sample, col = clst )

補助公式

問題

期待値

分散

繰り返し期待値の法則

証明

繰り返し分散の法則

証明

参考

感想

受験に臨むにあたって(勉強以外編)

成績

勉強法

書籍

統計検定特化型の書籍

統計学全般の書籍

買ったけど役に立ったか微妙なライン

webサイト

理論編

例：一様分布に従う2 つの確率変数の和

確率変数の変換

同時確率密度関数

確率変数のとりうる領域

領域の書き方補足

周辺確率密度関数

参考

準備

確認

問5

関数

実行

コメント

問6

関数

実行