理解したいこと

①ある繰り返し起こるイベントに対してn番目の発生時刻を $\displaystyle T_n$ とみれば、 $\displaystyle N_t$ は時刻tまでに起こるイベントの回数を表す確率過程とみなせる。
② $\displaystyle P(N_t = k ) = P(T_k \le t) - P(T_{k+1} \le t )$

①のお気持ちをくしゃみを通じて理解する

ある繰り返し起こるイベント → くしゃみ
k番目の発生時刻 → k回目のくしゃみが出た時刻
ここで k = 5 、 t = 11:00 とすると
- $\displaystyle N_{11:00} = 5$ は、11:00までに合計くしゃみ回数が5回となったことを表している。
- $\displaystyle T_{5} =$ 11:00 は、5回目のくしゃみが出た時刻が11:00だということを表している。
- 疑問）11:00は確かに時刻であるが数学的な表記としては微妙なのでは？
  - 回答）適当な日付(例：2022-03-28)を時刻に添えてからunix epoch time に脳内変換すれば時刻は整数となるので、そういう風に解釈すればよし。

計数過程と正値確率変数列の読み替え

$\displaystyle N_t \ge k \iff T_{k} \le t$
日本語訳：「時刻tまでの合計イベント回数がk回以上であること」と「k回目のイベント発生時刻が時刻t以前であること」は同じ(事象を別の視点で述べている)
具体例：11:00までに合計くしゃみ回数が5回以上であること vs 5回目のくしゃみは11:00までに発生している
具体例の深掘り：11:00までに合計くしゃみ回数が5回以上である、ということは10:45に合計くしゃみ回数は5回でその後6回目を10:46、7回目を10:59といったイベントを、「11:00までに合計くしゃみ回数が5回以上である」という文章は含んでいる。

②を理解したいのでお気持ちを読み取る

$P( N_t = k )$ を直接求めないのはなぜ？

それを知るために計算しているから。p.119の上にはポアソン分布に従う、と書いてある。p.119の中段以降はこれを導出するための式の羅列である。p.120あたりでガンマ分布をガシガシ計算することでポアソン分布になることが書いてある。なので結論だけ知りたいのであれば途中の式はスルーしても良いかもしれない。
なぜ $P(T_k \le t) - P(T_{k+1} \le t )$ と引き算しているのか
- まず、確率変数列Tは指数分布をごにょごにょしてガンマ分布に従うらしい。指数分布もガンマ分布も連続型確率分布であるため、確率変数が範囲ではなく1点を取る確率は0となる。たとえばXが標準正規分布に従う確率変数であるとして、X = 2となる確率は0であることと似た理屈である。ということで、確率変数列Tに注目すると等号ではなく不等号が現れそうな気配が感じ取れる。
- 次に、確率を引き算するときは包含関係が隠れている可能性があって、包含関係のうち共通部分を差し引いているかもしれない(直感)
  - くしゃみの例で言えば、
    - 11:00に合計くしゃみ回数が5回である
  - を
    - 5回目のくしゃみをした時刻が11:00以前である
    - 6回目のくしゃみをした時刻が11:00以前である
  - の二つを駆使して、 11:00までに合計くしゃみ回数が5回であるを表している、と見れば良い。
図示すると以下である。

2022-03-26

統計学実践ワークブック第15章確率過程の基礎 p.117のεiの分布を導出する

統計学実践ワークブック

はてなブログで書こうとしたものの、添字が付いた添字をはてなブログのTeX表記ではできなさそうだったのでSpeaker Deckにアップロードした。

f:id:axjack:20220326161127j:plain

speakerdeck.com

2022-03-17

統計学実践ワークブック第12章一般の分布に関する検定法 p.92 の尤度比検定を用いる場合の棄却域を導出する

統計学実践ワークブック

母比率の検定に関する話題で統計学実践ワークブックp.91は二項分布から話が始まる。そしてp.92にて尤度比検定の話となるが、導出過程は書いていなかったので自力で導出してみることにした。なお以下、二項分布ではなくベルヌーイ分布を用いるのは計算のしやすさとわかりやすさからである。

ベルヌーイ分布に従うn個の確率変数から最尤推定量を求める
- 尤度関数を立式する
- 最尤推定量を求める
尤度比のお気持ち
実際に尤度比を求めてみる
尤度比から対数尤度比の2倍(逸脱度)を求める

ベルヌーイ分布に従うn個の確率変数から最尤推定量を求める

尤度関数を立式する

$\displaystyle X_1,\cdots, X_n$ は独立にベルヌーイ分布 $Bern(\theta)$ に従う確率変数であるとする。 $X_i$ は確率θで1を確率1-θで0の値を取る。このとき尤度関数は $\displaystyle L(\theta) = P(X_1) P(X_2) \cdots P(X_n)$ となる但し $\displaystyle P(X_i ) = \theta^{X_i}(1-\theta)^{1-X_i}$ である。

尤度関数を変形すると、

$\displaystyle L(\theta) = P(X_1) P(X_2) \cdots P(X_n)$

$\displaystyle = \theta^{X_1}(1-\theta)^{1-X_1} \theta^{X_2}(1-\theta)^{1-X_2} \cdots \theta^{X_n}(1-\theta)^{1-X_n}$

$\displaystyle = \theta^{X_1 + X_2 + \cdots + X_n} (1-\theta)^{n - ( X_1 + X_2 + \cdots + X_n) }$

$\displaystyle = \theta^{n \bar{X} } (1-\theta)^{n - n\bar{X} }$

が得られる( $\displaystyle \bar{X} = \frac{1}{n} \sum X_i$ )。

最尤推定量を求める

さてここで最尤推定量を求めたいので、

尤度関数の対数すなわち対数尤度関数 $logL(\theta)$ を
$\theta$ で偏微分し
それを0とおいたものを $\theta$ について解く

という手順を踏もう。

対数尤度関数

$\displaystyle log L(\theta) = log \Big( \theta^{n \bar{X} } (1-\theta)^{n - n\bar{X} } \Big)$

$\displaystyle = log \Big( \theta^{n \bar{X} } \Big) + log \Big( (1-\theta)^{n - n\bar{X} } \Big)$

$\displaystyle = n \bar{X} \ log(\theta) + ( {n - n\bar{X} } ) \ log (1-\theta)$

対数尤度関数をθで偏微分

$\displaystyle \frac{\partial }{\partial \theta } log L(\theta)= \frac{\partial }{\partial \theta } \Big( n \bar{X} \ log(\theta) + ( {n - n\bar{X} } ) \ log (1-\theta) \Big)$

$\displaystyle = n \bar{X} \frac{1}{\theta} + ( {n - n\bar{X} } ) \frac{-1}{1 - \theta}$

対数尤度関数をθで偏微分 = 0 をθについて解く

$\displaystyle \frac{\partial}{\partial \theta} log L(\theta) = 0$

$\displaystyle \iff n \bar{X} \frac{1}{\theta} + ( {n - n\bar{X} } ) \frac{-1}{1 - \theta} = 0$

$\displaystyle \iff n \bar{X} (1 - \theta) + ( n\bar{X} - n ) \theta = 0$

$\displaystyle \iff n \bar{X} - n \bar{X} \theta + n\bar{X} \theta - n \theta = 0$

$\displaystyle \iff n \bar{X} - n \theta = 0$

$\displaystyle \iff \theta = \bar{X} \ ( = \hat{ \theta } )$

となって、最尤推定量 $\displaystyle \hat{\theta} = \bar{X}$ を得る。

尤度比のお気持ち

今回のポイントはここである。

f:id:axjack:20220317214013j:plain

尤度比は

$max \ L(\theta; H_0)$ ：帰無仮説のもとでの尤度関数の最大値
$max \ L(\theta; H_1)$ ：対立仮説のもとでの尤度関数の最大値

を使って、

$\displaystyle \lambda(X) = \frac{max \ L(\theta; H_1)}{max \ L(\theta; H_0)}$

と表される統計量である。正確性を『超』度外視すれば*1、

：帰無仮説のもとでの尤度関数の最大値
- ⇒ 尤度関数の $\theta$ に帰無仮説で与えられている $\theta_0$ を代入したもの
：対立仮説のもとでの尤度関数の最大値
- ⇒ 尤度関数の $\theta$ に最尤推定量 $\hat{ \theta }$ を代入したもの

を使って、

$\displaystyle \lambda(X) = \frac{L( \theta = \hat{\theta} )}{ L( \theta = \theta_0 )}$

となる。

実際に尤度比を求めてみる

$\displaystyle \lambda(X) = \frac{L( \theta = \hat{\theta} )}{ L( \theta = \theta_0 )}$

$\displaystyle = \frac{ \hat{\theta}^{n \bar{X}}(1-\hat{\theta})^{n - n\bar{X} }} { {\theta_0}^{n \bar{X}}(1-{\theta_0})^{n - n\bar{X} }}$

尤度比から対数尤度比の2倍(逸脱度)を求める

対数尤度比の2倍： $2 log \lambda(X)$ は 逸脱度*2 という名前がついているらしい。では以下にて逸脱度を計算すると、

$\displaystyle 2 log \lambda(X) = 2 log \Big( \frac{ \hat{\theta}^{n \bar{X}}(1-\hat{\theta})^{n - n\bar{X} }} { {\theta_0}^{n \bar{X}}(1-{\theta_0})^{n - n\bar{X} }} \Big)$

$\displaystyle = 2 log \Big( \Big( \frac{ \hat{\theta} }{\theta_0}\Big) ^{n \bar{X}} \Big( \frac{(1-\hat{\theta})}{(1-\theta_0)}\Big)^{n - n\bar{X}} \Big)$

$\displaystyle = 2 n\Big( \bar{X} log \Big( \frac{ \hat{\theta} }{\theta_0}\Big) + (1-\bar{X})log\Big( \frac{1-\hat{\theta}}{1-\theta_0} \Big) \Big)$

ここで、 $\hat{\theta} = \bar{X}$ より

$\displaystyle = 2 n\Big( \hat{\theta} log \Big( \frac{ \hat{\theta} }{\theta_0}\Big) + (1- \hat{\theta} )log\Big( \frac{1-\hat{\theta}}{1-\theta_0} \Big) \Big)$

となってp.92 の尤度比検定を用いる場合の棄却域を得ることができた。

*1: (言い訳)勉強中ゆえ自信がないため

*2:統計学実践ワークブック、平均・分散から始める一般化線形モデル入門、一般化線形モデル入門などを参照

2022-03-17

統計学実践ワークブック第12章一般の分布に関する検定法問12.2の[4] あてはまりのよさについて

統計学実践ワークブック R

やること

統計学実践ワークブック第12章一般の分布に関する検定法問12.2の[4] あてはまりのよさについて考えてみる。

情報整理

得られたデータについて

A) まとめる前
- 自由度：9
- カイ二乗統計量：16.37
- P-値：0.05954566
B) まとめた後
- 自由度：5
- カイ二乗統計量：2.27
- P-値：0.8106628

図示

赤がA(まとめる前)で、青がB(まとめた後)のカイ二乗分布で、塗りつぶし部分がP-値の範囲である。(赤塗りつぶしがおよそ0.05で、青塗りつぶしがおよそ0.8) f:id:axjack:20220317134020p:plain

カイ二乗分布上側確率表

自由度＼上側確率	0.025	0.05	0.10	0.5	0.8
9	19.02	16.92	14.68	8.34	5.38
5	12.82	11.07	9.23	4.35	2.34

結果の比較

適合度検定の帰無仮説は「観測度数が期待度数に適合している」である。したがって、

帰無仮説を棄却する
- 「観測度数が期待度数に適合している」とは言えない
- 帰無仮説を棄却するに足るデータが得られた
- 適合していない
- 当てはまっていない
帰無仮説を棄却しない
- 「観測度数が期待度数に適合している」と言えないこともない
- 帰無仮説を棄却するに足るデータが得られなかった
- 適合していることは棄却しない
- 当てはまっている

と結論づけたい(よくある言い回しのまとめ、願望)。

以上を考えると、P-値が大きい方が(ある有意水準から導出される棄却域に入っていないという意味では)比較的あてはまりがよいと思われる。結果、B)まとめた後の方が(今回の問題で言えばパラメータλ=2.99のポアソン分布に)比較的あてはまりがよいと考えられる。あくまで比較的であってストレートに「あてはまっている」と言ってはいけないところが統計学の言い回しなところに留意したい。

一方ワークブックでは

この結論に対して、上側10%点より大きいか小さいかで判断している。これは、

P-値を直接求めなくとも自由度に応じたカイ二乗上側パーセント点を使えばP-値の大小関係は分かる
どのような有意水準であれば棄却できるのかできないのか
適合度検定において棄却するとは棄却しないとはどのような意味なのか

を学び取れというメッセージなのかもしれない。

付録：ソースコード

# グラフ作成用関数
fdraw <- function(df,from,to,col,add,chisq_stat, ylim = c(0, 0.2) ){
  # 自由度 = df のカイ二乗分布
  curve(dchisq(x, df), from, to, add = add, col = col, xlab = '', ylab = '', ylim=ylim)

  # カイ二乗統計量
  points(chisq_stat, 0, col=col)
  
  # 上側確率の塗りつぶし
  rng <- seq(chisq_stat,to,0.2)
  segments(rng, 0, rng, dchisq(rng, df = df), col = col)
  
  # P-値
  print(paste("自由度",df,", カイ二乗統計量",chisq_stat, " のP-値は",
              pchisq(chisq_stat, df, lower.tail = F)
  ))
}


# グラフ作成
fdraw(df=9, from=0, to=20, col='red',add = F,  chisq_stat = 16.37)
fdraw(df=5, from=0, to=20, col='blue',add = T, chisq_stat = 2.27)


# カイ二乗分布上側確率表
qchisq( c(0.025, 0.05, 0.1,0.5,0.8) , df = 9, lower.tail = F)
qchisq( c(0.025, 0.05, 0.1,0.5,0.8) , df = 5, lower.tail = F)

2022-02-27

pythonのvenv：仮想環境

python

仮想環境ってなに？

グローバル環境を汚さずにパッケージとかをインストールできる環境のこと本家ドキュメントはこちら

仮想環境の作り方

python3 -m venv myenv

仮想環境の起動

axjack@axjack py % source myenv/bin/activate

pipが古いと怒られる

なぜデフォルトのpipが古いのかどうしたらupgradeできるのか、はよくわからない。。

(myenv) axjack@axjack py % pip list
Package    Version
---------- -------
pip        19.2.3 
setuptools 41.2.0 
WARNING: You are using pip version 19.2.3, however version 22.0.3 is available.
You should consider upgrading via the 'pip install --upgrade pip' command.

言われた通りpipをupgrade

(myenv) axjack@axjack py % pip install --upgrade pip
(myenv) axjack@axjack py % pip list
Package    Version
---------- -------
pip        22.0.3
setuptools 41.2.0

requiremenets.txtを使ってインストール

以前作った仮想環境のrequirements.txtを使って、

(myenv) axjack@axjack py % cat requirements.txt|head
appnope==0.1.2
argon2-cffi==21.3.0
argon2-cffi-bindings==21.2.0
asttokens==2.0.5
attrs==21.4.0
backcall==0.2.0
bleach==4.1.0
cffi==1.15.0
cycler==0.11.0
debugpy==1.5.1

先ほど作った仮想環境にてpip installする。

pip install -r requirements.txt

pip listにて確認

(myenv) axjack@axjack py % pip list       
Package              Version
-------------------- -------
appnope              0.1.2
argon2-cffi          21.3.0
argon2-cffi-bindings 21.2.0
asttokens            2.0.5

うまくいったようだ。

jupyter notebookの起動はこんなかんじ

(myenv) axjack@axjack py % python -m notebook

デアクティベート

(myenv) axjack@axjack py % deactivate
axjack@axjack py %

requirements.txtを作成する

(myenv) axjack@axjack py % python -m pip freeze > requirements.txt

venvをきれいにする

axjack@axjack py % python3 -m venv --clear myenv

参考にしたURL

venvについて
venvをクリアする
- https://tekunabe.hatenablog.jp/entry/2018/12/28/venv_clear
pythonのimportのしくみ
- https://zenn.dev/panyoriokome/articles/f34ae72cc33150
jupyter notebookをインストール
- https://www.javadrive.jp/python/jupyter-notebook/index1.html
pipの更新
- https://www.curict.com/item/5a/5ac72d2.html
- https://ytyaru.hatenablog.com/entry/2020/01/23/111111

昔の自分への追伸

あの時インストールしたnumpyとscipyは消しました。が、今回新規で作ったvenvの中でpip installしました。

(myenv) axjack@axjack lib % pwd            
/usr/local/lib
(myenv) axjack@axjack lib % ls | grep python
(myenv) axjack@axjack lib %

2021-12-31

ランダムウォークと単位根

統計

単位根を持つ時系列の例
$U_{t} = U_{t-1} + \varepsilon_{t}$
を可視化、および階差をとって可視化してみる。時系列データ分析p.98 より。

一次元ランダムウォーク

f:id:axjack:20211231232348p:plain

一次元ランダムウォークの階差

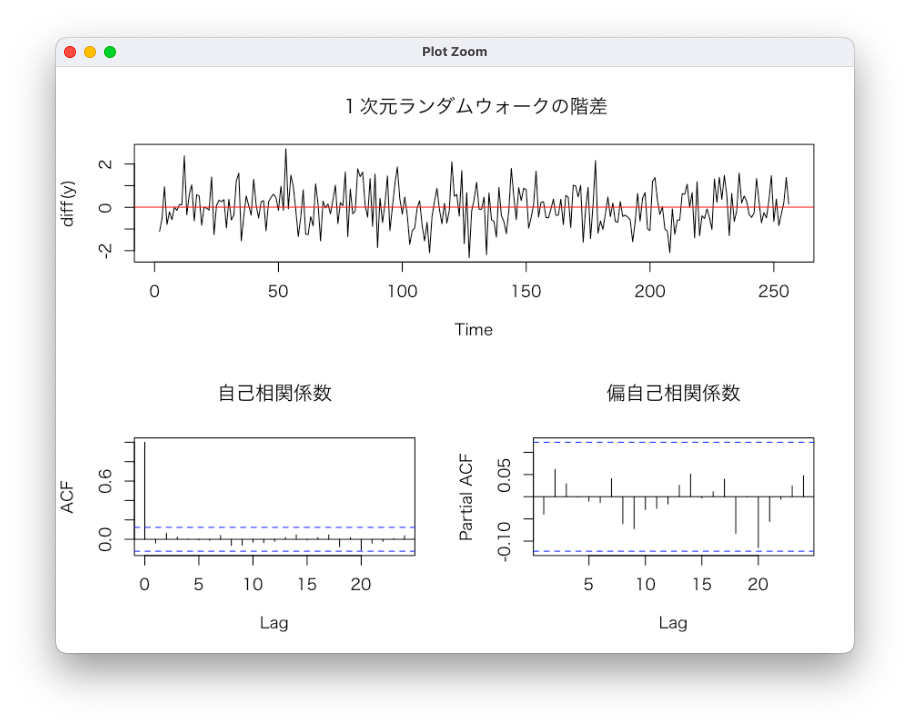
f:id:axjack:20211231232451p:plain

ADF検定の結果

ADF検定は単位根の有無を検定するもので、帰無仮説は「データ系列に単位根が存在する」である。
有意水準5%としてみると検定の結果、原系列(adf.test(y))の帰無仮説は棄却できなさそう。差分系列(adf.test(diff(y)))についてはp値 < 0.01より帰無仮説を棄却できそうである。

> adf.test(y)
Augmented Dickey-Fuller Test
data: y
Dickey-Fuller = -2.5377, Lag order = 6, p-value = 0.3494
alternative hypothesis: stationary

> adf.test(diff(y))
Augmented Dickey-Fuller Test
data: diff(y)
Dickey-Fuller = -5.6887, Lag order = 6, p-value = 0.01
alternative hypothesis: stationary
Warning message:
In adf.test(diff(y)) : p-value smaller than printed p-value

コード

# 単位根を持つ時系列データ
# p.98
# 一次元ランダムウォーク
y <- cumsum( rnorm(2^8) )
y <- ts(y)

dev.off()
par(family="HiraKakuProN-W3")
split.screen(c(2,1))
split.screen(c(1,2), screen = 2)
screen(1);plot(y, main = "１次元ランダムウォーク")
abline(h = mean(y), col="red")
screen(3);acf(y, main = "自己相関係数")
screen(4);pacf(y, main = "偏自己相関係数")

dev.off()
par(family="HiraKakuProN-W3")
split.screen(c(2,1))
split.screen(c(1,2), screen = 2)
screen(1);plot(diff(y), main = "１次元ランダムウォークの階差")
abline(h = mean(diff(y)), col="red")
screen(3);acf(diff(y), main = "自己相関係数")
screen(4);pacf(diff(y), main = "偏自己相関係数")

2021-12-31

ARとMAの自己相関係数と偏自己相関係数

統計学実践ワークブック

統計学実践ワークブックのp.248の表を、グラフにて確かめる。表27.1の内容を一部引用。

選択モデル	自己相関係数	偏自己相関係数
AR(1)	ゆっくりと減衰	2次以降0
MA(1)	2次以降0	ゆっくりと減衰
AR(2)	ゆっくりと減衰	3次以降0
MA(2)	3次以降0	ゆっくりと減衰

AR(1)とMA(1)

f:id:axjack:20211231184209p:plain

AR(2)とMA(2)

f:id:axjack:20211231184237p:plain

コード

rm(list=ls())

# 諸準備
dev.off()
par(family="HiraKakuProN-W3")
par(mfrow=c(2,2))

# AR(1)とMA(1) ####
y1 <- arima.sim(n=1000, list(ar=c(0.5))) 
y2 <- arima.sim(n=1000, list(ma=c(0.8))) 
y1 |> acf(main="AR(1)の自己相関係数")
y1 |> pacf(main="AR(1)の自己相関係数")
y2 |> acf(main="MA(1)の自己相関係数")
y2 |> pacf(main="MA(1)の偏自己相関係数")

# AR(2)とMA(2) ####
y3 <- arima.sim(n=1000, list(ar=c(0.4,0.2))) 
y4 <- arima.sim(n=1000, list(ma=c(0.8,0.4))) 
y3 |> acf(main="AR(2)の自己相関係数")
y3 |> pacf(main="AR(2)の自己相関係数")
y4 |> acf(main="MA(2)の自己相関係数")
y4 |> pacf(main="MA(2)の偏自己相関係数")

2021-12-30

時系列データ分析に登場する統計的仮説検定

統計

gihyo.jp

ということで、本書に出てくる統計的仮説検定をまとめます。

Shapiro-Wilkの検定

データが正規分布に従っているか否かの検定
正規性の検定
帰無仮説：対象データが正規分布に従う
p.61

連の検定

２値のデータの並びについて規則性の有無を確かめる検定
帰無仮説：+と-の並び方に規則性はない
p.62

Ljung-Box検定

自己相関関係の有無について判断する検定
帰無仮説：ラグkまでの自己相関係数が0である
p.80

Dickey-Fuller検定(ADF検定)

単位根の有無の検定
帰無仮説：データ系列に単位根が存在する
p.99

Kolmogorov-Smirnov検定

汎用的な適合度検定
２つの母集団確率分布が等しいか否かを、
標本から経験分布関数を作りそれを比較して調べる
帰無仮説：２つの母集団の確率分布は等しい
p.129