axjack's blog

### axjack is said to be an abbreviation for An eXistent JApanese Cool Klutz ###

2018年11月 統計検定2級 問9

勉強 復習

この問題をなぜ解くのか

前にこんなこと

統計検定であって確率検定ではないので、サイコロを７回投げる時２以下の目が出る確率を解けるようになってもなんだかなぁ

統計検定２級に合格したので勉強法やら参考書などを書いておきます。 - axjack's blog

を書きました。がしかし、統計検定 準1級の勉強をしていく中「やっぱ確率もちゃんと解けないとダメじゃん😢」と気持ちが一転したので改めてちゃんと解いてみようと思った次第です。

問題文の概要

どの面も等確率で出る6面のサイコロを7回投げる。2以下の目が出る回数をXとする。

  • 問(1)：P(X = x+1)とP(X = x)の比、i.e. \frac{ P(X=x+1) }{ P(X=x) }を求めよ
  • 問(2)：P(X = x) が最大となるxは?

解答

問(1)

\displaystyle X_i を出目が2以下の時に1、そうでない時を0とすると\displaystyle X_iはベルヌーイ分布：Bin(1,p)に従う。ここでp=1/3である。この時、\displaystyle X = \sum X_i は二項分布：Bin(n,p)に従う。よって、確率質量関数は\displaystyle P(X=k)= {}_n \mathrm{ C }_k p^{k} (1-p)^{n-k} となる。ここで、n=7, p=1/3を代入するとP(X=x)とP(X=x+1)はそれぞれ、

\displaystyle P(X=x) = {}_7 \mathrm{ C }_x (1/3)^x (2/3)^{7-x}
\displaystyle P(X=x+1) = {}_7 \mathrm{ C }_{x+1} (1/3)^{x+1} (2/3)^{7-(x+1)}

となる。すると、

\displaystyle \frac{P(X=x+1)}{P(X=x)} \\ \displaystyle = \frac{ {}_7 \mathrm{ C }_{x+1} (1/3)^{x+1} (2/3)^{7-(x+1)} } { {}_7 \mathrm{ C }_x (1/3)^x (2/3)^{7-x} } \\ \displaystyle = \frac{ {}_7 \mathrm{ C }_{x+1} (1/3)^{x} (1/3) (2/3)^{7-x} (2/3)^{-1} } { {}_7 \mathrm{ C }_x (1/3)^x (2/3)^{7-x} } \\ \displaystyle = \frac{ \frac{ 7! }{ (7-(x+1))! (x+1)! } (1/3)^{x} (1/3) (2/3)^{7-x} (2/3)^{-1} }{ \frac{7!}{(7-x)!x!} (1/3)^x (2/3)^{7-x} }\\ \displaystyle = \frac{ \frac{ 7! }{ (6-x)! (x+1)x! } (1/3)^{x} (1/3) (2/3)^{7-x} (2/3)^{-1} }{ \frac{7!}{(7-x)(6-x)!x!} (1/3)^x (2/3)^{7-x} } \\ \displaystyle = \frac { \frac{ 1 }{ x+1 } (1/3) (3/2) }{ \frac{1}{7-x} } = \frac{ 7-x }{ 2x+2 }

となる。よって、 \displaystyle \frac{P(X=x+1)}{P(X=x)} = \frac{ 7-x }{ 2x+2 }

問(2)

P(X=x)が最大となるxを \displaystyle \frac{P(X=x+1)}{P(X=x)} = \frac{ 7-x }{ 2x+2 } = Q(x) を用いて考えてみると、Q(x)が1より大であればP(X=x+1) > P(x)であると言えるし1未満であればP(X=x+1) < P(x)と言える。具体的にxへ0から6を代入すると、

x Q(x) 判定
0 7/2 > 1 P(1) > P(0)
1 6/4 > 1 P(2) > P(1)
2 5/6 < 1 P(3) < P(2)
3 4/8 < 1 P(4) < P(3)
4 3/10 < 1 P(5) < P(4)
5 2/12 < 1 P(6) < P(5)
6 1/14 < 1 P(7) < P(6)

となる。関数の増減表のように判定の列を眺めれば、P(x)はP(2)がピークであることからP(X = x) が最大となるxは2である。

超幾何分布

統計 勉強 復習 R

何度やっても忘れるのでブログに書いて覚えよう。

超幾何分布の確率質量関数

\displaystyle P(X=x) = f(x; N,M,n) = \frac{ \binom{M}{x} \binom{N-M}{n-x} } { \binom{N}{n} }

計算例

その1

男50人女50人から10人を選ぶ。10人のうち男3人女7人となる確率pは、超幾何分布を用いて

\displaystyle p = \frac{ \binom{50}{3} \binom{50}{7} }{ \binom{100}{10}}

その2

統計検定準一級2017年問10より引用。表の80人から30人を無作為抽出する。その30人のうち男性かつ就職している人数Xは超幾何分布に従う。

＼ 就職 非就職 計
男性 38 3 41
女性 30 9 39
計 68 12 80
  • 80人から30人を選ぶ
  • 「男性かつ就職」である人：38
  • 「男性かつ就職」でない人：80-38 = 42

と整理して、
\displaystyle P(X=x) = \frac{ \binom{38}{x} \binom{42}{30-x} }{ \binom{80}{30} }

となる。

その3

同じ表を用いて、80人から20人を無作為抽出する。その20人のうち「女性かつ非就職」な人数Xは超幾何分布に従う。

  • 80人から20人を選ぶ
  • 「女性かつ非就職」である人：9
  • 「女性かつ非就職」でない人：80-9 = 71

と整理して、
\displaystyle P(X=x) = \frac{ \binom{9}{x} \binom{71}{20-x} }{ \binom{80}{20} }

となる。

Rで計算する

choose関数で立てた式が超幾何分布の質量関数dhyperと同じことを確認。

# その1
> choose(50,3)*choose(50,7)/choose(100,10)
[1] 0.1130964
> dhyper(3,50,50,10)
[1] 0.1130964

dhpyer(x,m,n,k)の引数*1は、

  • x: vector of quantiles representing the number of white balls drawn without replacement from an urn which contains both black and white balls.
  • m: the number of white balls in the urn.
  • n: the number of black balls in the urn.
  • k:the number of balls drawn from the urn.

*1:https://www.rdocumentation.org/packages/stats/versions/3.6.1/topics/Hypergeometric

連の検定(Runs Test for Detecting Non-randomness)

統計 調べ物 R

はじめに

連の検定についてよく分からなかったのでRで実装して確かめてみました。

連とは？

２値{A,B}を取る系列ABAABBAAABBBABがあった時、これをA | B | AA | BB | AAA | BBB | A | Bと連続する同じ値ごとに分割できるように見える。この時同じ文字または記号のひと続きを連(run)*1と言い、またひと続きの個数を連の長さ*2と言う。この場合、Aの連が4つ(= {A,AA,AAA,A})とBの連が4つ(= {B,BB,BBB,B})あることが分かる。AAAAAAAAABBBBBBBBBBBであれば、Aの連が1つでBの連が1つとなる。

確かめたこと

Aの数(= Na)とBの数(= Nb)が与えられた時、N = Na+Nbの大きさを持つ系列は、

  • もしA・Bがランダムに現れるなら(←帰無仮説)連の数はどのような分布になるのか　→　正規分布
  • 連の数の平均値・分散が以下の式*3どおりとなるか

f:id:axjack:20190926230103p:plain

を確かめた。

ソース

# 連の検定####
rm(list=ls())

# --------------------
# 関数: generateRun ####
# --------------------
# 引数
#   Na_: Aの個数
#   Nb_: Bの個数
# 戻り値
#   連の数を返す関数
# --------------------
generateRun <- function(Na_, Nb_){
  return(
      function(dummy){
        N <- Na_ + Nb_
        Arep <- rep(TRUE,Na_)
        Brep <- rep(FALSE,Nb_)
        AB <- c(Arep,Brep)
        xx <- sample(AB, N, replace = FALSE)
        yy <- xx[1:(N-1)]
        zz <- xx[2:N]
        return( sum( yy != zz)  + 1 )
    }
  )
}

# シミュレーション ####
## 各種変数設定
Na <- 9 # Aの個数
Nb <- 11 # Bの個数
sim_N <- 10000 # シミュレーション回数

## 平均値と分散
( t_mean <- (2*Na*Nb)/(Na+Nb) + 1 ) # 平均値
( t_var <- (2*Na*Nb*(2*Na*Nb - Na - Nb))/((Na+Nb)^2 * (Na+Nb-1)) ) # 分散

# シミュレーション実行
Result.Run <- sapply( 1:sim_N, generateRun(Na,Nb) )

# 要約
table(Result.Run)
summary( Result.Run )
var( Result.Run )

# グラフ表示
hist(Result.Run,breaks = seq(min(Result.Run),max(Result.Run),1))
par(new=T)

# 正規分布を重ね合わせ
curve(dnorm(x,t_mean,sqrt(t_var)),min(Result.Run),max(Result.Run),xlab="",ylab="",xaxt="n", yaxt="n",col="red",bty="n")

結果の確認

数値の確認

> # シミュレーション ####
> ## 各種変数設定
> Na <- 9 # Aの個数
> Nb <- 11 # Bの個数
> sim_N <- 10000 # シミュレーション回数
> ## 平均値と分散
> ( t_mean <- (2*Na*Nb)/(Na+Nb) + 1 ) # 平均値
[1] 10.9
> ( t_var <- (2*Na*Nb*(2*Na*Nb - Na - Nb))/((Na+Nb)^2 * (Na+Nb-1)) ) # 分散
[1] 4.637368
> # シミュレーション実行
> Result.Run <- sapply( 1:sim_N, generateRun(Na,Nb) )
> # 要約
> table(Result.Run)
Result.Run
   2    3    4    5    6    7    8    9   10   11   12   13   14   15   16   17   18 
   1    3   13   28  167  312  852 1218 1725 1699 1699 1144  704  279  121   30    5 
> summary( Result.Run )
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   2.00    9.00   11.00   10.89   12.00   18.00 
> var( Result.Run )
[1] 4.666794

プロット

f:id:axjack:20190926230756p:plain

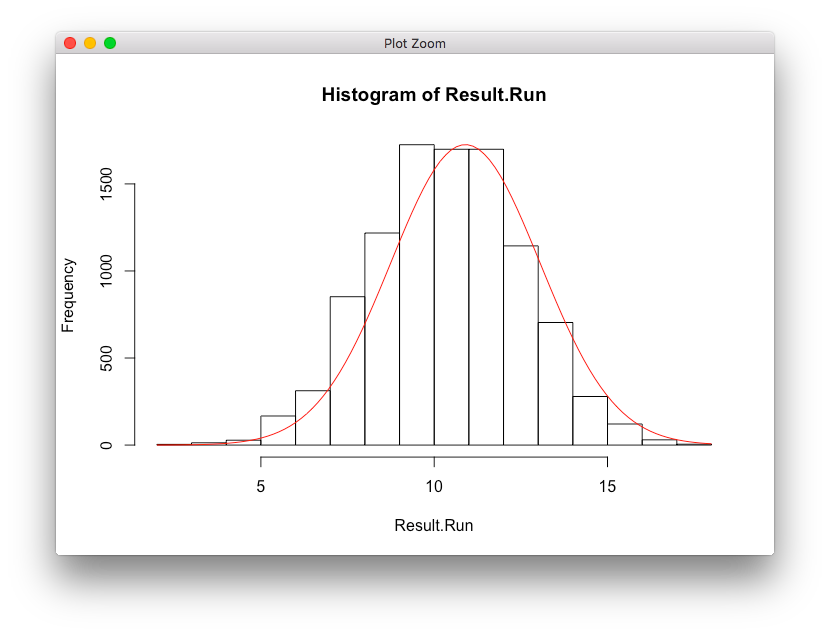
結果の考察

  • 計算した平均値・分散がシミュレーションの結果とだいたい合っていることがわかった。
  • ヒストグラムとカーブプロットが大まかにあっている。

おわりに

帰無仮説の下での平均値・分散の式が奇妙で覚えられないし式を見てもあまり実感が湧かなかったものの、シミュレーションしてみると確かに平均値・分散がそれっぽく合うのでこの式の妥当性を確認することができた。疑わしい系列があってもこれで確かめることができそうだ。

参考

連の検定関連

R言語のplot関連

*1:[連の検定]より引用

*2:[連の検定]より引用

*3:式は[連の検定]より引用

2019年8月をワールドワイドに考える

メモ プログラミング 調べ物

はじめに

UTCを考慮すると途端にわけわからなくなったので整理する。

UTCとは

wikiで協定世界時 - Wikipediaをみませう。

UTCってプラマイいくつまであるの？

時間帯 (標準時) - WikipediaによるとからUTC-12からUTC+14まである。日本はUTC+9

2019年8月をUTCで列挙する

以下の時間帯で考える。

すると次の表のようになる

UTC-12 UTC0 UTC+9 UTC+14
7/30 22:00 7/31 10:00 7/31 19:00 8/01 00:00
7/31 03:00 7/31 15:00 8/01 00:00 8/01 05:00
7/31 03:00 8/01 00:00 8/01 09:00 8/01 14:00
8/01 00:00 8/01 12:00 8/01 21:00 8/02 02:00
… … … …
8/30 22:00 8/31 10:00 8/31 19:00 9/01 00:00
8/31 03:00 8/31 15:00 9/01 00:00 9/01 05:00
8/31 03:00 9/01 00:00 9/01 09:00 9/01 14:00
9/01 00:00 9/01 12:00 9/01 21:00 9/02 02:00

結局2019年8月とは

  • UTC+14が世界で最も早く8/1を迎えるので、UTC0で考えれば7/31 10:00(⇔日本時間 7/31 19:00)
  • UTC-12が世界で最も遅く9/1を迎えるので、UTC0で考えれば9/1 12:00(⇔日本時間 9/1 21:00)

の時間帯を抽出すればとりあえず取りこぼすことはなさそうだ。

参考

タイムゾーンを考慮した日時の扱いのベストプラクティス - エムスリーテックブログ

久保川『現代数理統計学の基礎』p.25 命題2.21 (平方変換)

統計 確率

やること

確率変数Xの確率密度関数をf_X(x)とする。 Xの平方変換Y=X^2に対して、Yの密度関数は？
という命題について、式変形の行間を埋めます。

以下途中式

y >0に対して\{x|x^2 \le y\} = \{x|-\sqrt{y} \le x \le \sqrt{y} \} であるから

\displaystyle f_Y (y) = \frac{d}{dy} P( X \in \{ x|x^2 \le y\} ) \\\\ \displaystyle = \frac{d}{dy} \int_{-\sqrt{y}}^{\sqrt{y}} f_X (x) dx \\\\ \displaystyle = \frac{d}{dy} \Bigl( F_X(\sqrt{y}) - F_X(-\sqrt{y}) \Bigr) \\\\ \displaystyle = f_X(\sqrt{y})\frac{d}{dy}(\sqrt{y}) - f_X(-\sqrt{y})\frac{d}{dy}(-\sqrt{y}) \\\\ \displaystyle = f_X(\sqrt{y})\frac{1}{2\sqrt{y}} - f_X(-\sqrt{y})\frac{-1}{2\sqrt{y}} \\\\ \displaystyle = f_X(\sqrt{y})\frac{1}{2\sqrt{y}} + f_X(-\sqrt{y})\frac{1}{2\sqrt{y}} \\\\ \displaystyle = \Bigl( f_X(\sqrt{y}) + f_X(-\sqrt{y}) \Bigr)\frac{1}{2\sqrt{y}}

と無事式変形できる。

多変量解析法入門pp.52-53のテコ比の式変形

統計 勉強

やること

多変量解析法入門p.52の式(4.35)あたりの式変形の行間を埋めてみる。

式変形

式(4.35)にて
\begin{eqnarray} \hat{y_k} &=& \hat{\beta_0} + \hat{\beta_1}x_k \\ &=& \bar{y} + \hat{\beta_1}(x_k - \bar{x} ) \\ &=& \frac{\Sigma y_i}{n} + \frac{ (x_k - \bar{x}) \Sigma(x_i-\bar{x})y_i }{ S_{xx} } \end{eqnarray}


ここで、上式の第一項は

\displaystyle \frac{\Sigma y_i}{n} = \frac{1}{n}y_1 + \frac{1}{n}y_2 + \cdots + \frac{1}{n}y_k + \cdots + \frac{1}{n}y_n \\ \displaystyle = \begin{bmatrix} y_1 & y_2 & \cdots & y_k & \cdots & y_n \end{bmatrix} \begin{bmatrix} \frac{1}{n} & \frac{1}{n} & \cdots & \frac{1}{n} \end{bmatrix}'


第二項は

\displaystyle \frac{ (x_k - \bar{x}) \Sigma(x_i-\bar{x})y_i }{ S_{xx} } = \Bigl( \frac{(x_k - \bar{x} )}{S_{xx}} \Bigr) \Bigl( (x_1-\bar{x})y_1 + (x_2-\bar{x})y_2 + \cdots + (x_n-\bar{x})y_n \Bigr) \\ \displaystyle = \begin{bmatrix} y_1 & y_2 & \cdots & y_k & \cdots & y_n \end{bmatrix} \begin{bmatrix} \Bigl( \frac{(x_k-\bar{x})(x_1 - \bar{x})}{S_{xx}} \Bigr) & \Bigl( \frac{(x_k-\bar{x})(x_2 - \bar{x})}{S_{xx}} \Bigr) & \cdots & \Bigl( \frac{(x_k-\bar{x})(x_k - \bar{x})}{S_{xx}} \Bigr) & \cdots & \Bigl( \frac{(x_k-\bar{x})(x_n - \bar{x})}{S_{xx}} \Bigr) \end{bmatrix}'


より、バラバラにした項を足して元に戻せば、

\displaystyle \hat{y_k} = \begin{bmatrix} y_1 & \cdots & y_k & \cdots & y_n \end{bmatrix} \begin{bmatrix} \Bigl( \frac{1}{n} + \frac{(x_k-\bar{x})(x_1 - \bar{x})}{S_{xx}} \Bigr) & \cdots & \Bigl( \frac{1}{n} + \frac{(x_k-\bar{x})(x_k - \bar{x})}{S_{xx}} \Bigr) & \cdots & \Bigl( \frac{1}{n} + \frac{(x_k-\bar{x})(x_n - \bar{x})}{S_{xx}} \Bigr) \end{bmatrix}' \\ \displaystyle \iff \hat{y_k} = \begin{bmatrix} y_1 & \cdots & y_k &\cdots& y_n\end{bmatrix} \begin{bmatrix} h_{k1} & \cdots & h_{kk} & \cdots & h_{kn} \end{bmatrix}'


となる。

ということで、y_kの係数

\displaystyle h_{kk} = \frac{1}{n} + \frac{ (x_k - \bar{x})^2 }{ S_{xx} }

をテコ比と呼ぶ。式(4.36)

とりあえずアソシエーション分析する〜その３〜

調べ物 統計

手を動かして形は理解したっぽいので、今度こそ(？)仕組みを理解する編です。いきなり読むと分からなくなるので、何となくアソシエーション分析のパッケージ{arules}は動かせたけどイマイチ意味がわからないんだよなーという状態になった時に読むのをお勧めします。


前回↓
axjack.hatenablog.jp

もくじ

アソシエーション分析の内部で使っているデータはどんな形式なのか？

アソシエーション分析の内部で使っているデータとは、{arules}のread.transactions関数で読み込んだものを指しています。この読み込んだデータをSQLで喩えてみるべく、TransというSQLのテーブルにアソシエーション分析の内部で使っているデータが入っているとします。関係スキーマ表記とcreate table 表記を用いてTransテーブルを表すと、以下のようになります。なおここで、アイテムが全部でp種類あるとしましょう。

関係スキーマ表記

Trans( tranID, item_1, item_2, ..., item_p )
となります。下線部は主キーです。

create table 表記

create table Trans(
    tranID nvarchar(max) not null primary key
  , item_1  bit not null
  , item_2 bit not null
  , ...
  , item_p bit not null
);

となります。

記号Mと演算子σを定義する

ここで唐突ですが、記号Mと演算子σをSQLを用いて定義します。
なお、記号「:=」は「左辺を右辺で定義する」、記号「=」は「左辺と右辺は等しい・上の式と右の式は等しい」と解釈してください。

記号M は Transの全行数

記号M は Transの全行数を表します。select文で書くと、

M := select count(*) from Trans;

となります。

演算子σ は Transの抽出条件つきの行数

幾つか例示します。ここでXやYはTransテーブルにあるtranIDではない任意の列(すなわちitem_1〜item_pのどれか)とします。

カッコの中が１つの場合

σ( X ) := select count(*) from Trans where X = 1;

カッコの中が２つの場合

σ( X∪Y ) := select count(*) from Trans where X = 1 and Y = 1;

σ( Y∪X ) := select count(*) from Trans where Y = 1 and X = 1;
= select count(*) from Trans where X = 1 and Y = 1;
= σ( X∪Y )

Xが複合アイテム( X = {X1, X2} )のような場合は、

σ( X ) = σ( {X1, X2} ) := select count(*) from Trans where X1 = 1 and X2 = 1;

となります。*1

相関ルールの３指標は何者なのか？

相関ルールの３指標とは、

  • Support(サポート; 支持度)
  • Confidence(コンフィデンス; 確信度)
  • Lift(リフト; リフト値)

を指します。

さて以下にて、σはSupport・Confidence・ Liftを用いて表せることを示します。

Support(サポート; 支持度)

Suppと略します。

Supp( X ) := σ(X) / M
より、σ(X) = Supp( X ) * M

Supp( X ⇒ Y ) := σ( X∪Y ) / M
より、σ( X∪Y ) = Supp( X ⇒ Y ) * M

ということで、SuppにMを掛けると「ルールが含まれるトランザクション数」を取り出せます。

Confidence(コンフィデンス; 確信度)

Confと略します。

Conf( X ⇒ Y ) := Supp( X ⇒ Y ) / Supp( X ) 
より、Supp( X ) = Supp( X ⇒ Y )/Conf( X ⇒ Y )
ところでSupp( X ) = σ( X ) / Mなので
σ( X ) = ( Supp( X ⇒ Y )/Conf( X ⇒ Y ) ) * M

ということで、SuppをConfで割ってからMを掛けると
「ルールの前件(X ⇒ YにおけるXの部分)が含まれるトランザクション数」が取り出せます。

Lift(リフト; リフト値)

Lift( X ⇒ Y ) := Conf( X ⇒ Y ) / Supp(Y) 
より、Supp( Y ) = Conf( X ⇒ Y )/Lift( X ⇒ Y )
ところでSupp( Y ) = σ( Y ) / Mなので
σ( Y ) = ( Conf( X ⇒ Y )/Lift( X ⇒ Y ) ) * M

ということで、ConfをLiftで割ってからMを掛けると
「ルールの後件(X ⇒ YにおけるYの部分)が含まれるトランザクション数」が取り出せます。


以上をまとめると、

σ Supp,Conf,Lift で表すと
σ( X∪Y ) Supp( X ⇒ Y ) * M
σ( X ) ( Supp( X ⇒ Y )/Conf( X ⇒ Y ) ) * M
σ( Y ) ( Conf( X ⇒ Y )/Lift( X ⇒ Y ) ) * M

となります。

これの何が嬉しいかというと、アソシエーション分析で得られたSupp・Conf・Liftの値を割り算掛け算することによって比率から個数に変換することができるわけです。(なぜならば「演算子σ は Transの抽出条件つきの行数」であるから、です。)

実際のデータで確かめてみる

アソシエーション分析(1)から表を２つ引用します。

表：トランザクション
f:id:axjack:20190806211933p:plain

表：アソシエーション分析の結果
f:id:axjack:20190806211949p:plain

いくつかのルールにてσを求めてみます。ここでM = 5とします。

例１

ルール lhs ⇒ rhs supp conf lift
6 ソーセージ ⇒ オムツ 0.2 1 1.66

は

σ( ソーセージ∪オムツ ) = supp * M = 0.2 * 5 = 1
σ( ソーセージ ) = (supp/conf) * M = (0.2/1) * 5 = 1
σ( オムツ ) = (conf/lift) * M = (1/1.666) * 5 = 3

となります。

例２

ルール lhs ⇒ rhs supp conf lift
11 タバコ ⇒ 弁当 0.2 1 2.5

は

σ( タバコ∪弁当 ) = supp * M = 0.2 * 5 = 1
σ( ソーセージ ) = (supp/conf) * M = (0.2/1) * 5 = 1
σ( オムツ ) = (conf/lift) * M = (1/2.5) * 5 = 2

となります。

例３

ルール lhs ⇒ rhs supp conf lift
17 {オムツ, ソーセージ } ⇒ ビール 0.2 1 1.25

は

σ( {オムツ, ソーセージ}∪{ビール} ) = supp * M = 0.2 * 5 = 1
σ( {オムツ, ソーセージ} ) = (supp/conf) * M = (0.2/1) * 5 = 1
σ( {ビール} ) = (conf/lift) * M = (1/1.25) * 5 = 4

となります。

おわりに

アソシエーション分析{arules}をいじって一週間ぐらい経過しました。支持度・確信度・リフト値の意味がわからずムムムとなっていた状態からはだいぶ進歩したような気持ちです。比率を個数に直すと結構「なるほど！」と思えてきました。

「アソシエーション分析してみたけど、比率だけだと実感が湧かない！」という人は比率を個数に直して考えると理解が深まるかもしれません。また、個数に直してみると「比率はどうなってるの？」とやっぱり比率が恋しく？なりますね笑　

こんなかんじで比率・個数を行き来していくとアソシエーション分析の面白さがより一層分かってくるのかなぁ、と感じました。

参考

en.wikipedia.org

www.cis.doshisha.ac.jp

*1:Association rule learning - Wikipediaによると、"Note that supp(X∪Y) means the support of the union of the items in X and Y. This is somewhat confusing since we normally think in terms of probabilities of events and not sets of items. " と書かれている。一見「∪」の記号からORを連想してしまうが決してそうではないということを注として書いておく。X∪Yに於けるXは集合でありYも集合である。すなわちX = {みかん,ビール}, Y = {ビール, おむつ} ならば X∪Y = {みかん, ビール, おむつ}である。(※ X∩Y は {ビール} なことに注意。) そして結果的にσ( X∪Y )をselect count(*)文に翻訳するとそれぞれのアイテムをbit型な列とした時に「=1」でandを使って結んだ抽出条件と同じになる。この場合はσ( X∪Y ) = select count(*) from Trans where みかん = 1 and ビール = 1 and おむつ = 1である。集合の要素と列で同じ名前を使っていることが混乱の原因なのかもしれないものの、そこは上手くLet's 脳内変換。

axjack is said to be an abbreviation for An eXistent JApanese Cool Klutz.