axjack's blog

### axjack is said to be an abbreviation for An eXistent JApanese Cool Klutz ###

2019年6月 統計検定準一級 問11

復習

問題の超大雑把な概要

詳細はお手元に問題を用意してください。

定数の情報：

\theta,\phi \in [0,1], \phi + \theta \le 1

推移確率行列M：

\begin{equation}M=\begin{pmatrix} 1-\theta & \theta & 0 \\\\ \theta & 1-\theta-\phi & \phi \\\\ 0 & \phi & 1-\phi \end{pmatrix} \end{equation}

問題

[1]

格付けの状態(A,B,C)を番号(1,2,3)に対応させ、 i,j \in \{1,2,3\} とする。ある年の格付けAが100社・格付けBが20社・格付けCが0社。翌年において、
・A→Bに推移した企業が5社
・B→Aに推移した企業が1社
・他に変化はなかった
・\phi = 0.01とする

このとき、\thetaの最尤推定値を、小数点第3位を四捨五入して答えよ。

[2]

Mの固有値をλとし、直交行列(U)_{ij}= u_{ij}を
\begin{equation}U^{T}MU = \begin{pmatrix} \lambda_{1} & 0 & 0 \\\\ 0 & \lambda_{2} & 0 \\\\ 0 & 0 & \lambda_{3} \end{pmatrix} \end{equation}
を満たすように取る。
t年に於いて格付けAの企業がt+nにおいて格付けCである確率を、n・λ・uを用いて表せ。

解答

[1]

ある年→翌年の格付けの変化は、

\begin{pmatrix} 95 & 5 & 0 \\\\ 1 & 19 & 0 \\\\ 0 & 0 & 0 \end{pmatrix}

と表される。求めたいのはθの最尤推定値である。確率は与えられている。確率分布は３項の状態を扱っているので多項分布の３項版とする。


多項分布の式は、\displaystyle Mult( m | \mu, N ) = \frac{N!}{m_{1}! \cdots m_{K}! } \prod_{k=1}^{K}\mu_{k}^{m_k} ただし N=\sum_{k=1}^K m_k

よって、尤度関数Lは

\displaystyle L = \frac{ (95+5+0)! }{95!5!0!} (1-\theta)^{95} \theta^{5} 0^0 \times \frac{ (1+19+0)! }{1!19!0!} \theta^1 (1-\theta-\phi)^{19} \phi^0 \times \frac{ (0+0+0)! } {0!0!0!} 0^0 \phi^0 (1-\phi)^0


\phi = 0.01*1を代入しながら整理すると、

\displaystyle L = \frac{ (100)! }{95!5!0!} (1-\theta)^{95} \theta^{5} 0^0 \times \frac{ (20)! }{1!19!0!} \theta^1 (1-\theta-0.01)^{19} (0.01)^0 \times \frac{ (0+0+0)! } {0!0!0!} 0^0 (0.01)^0 (1-0.01)^0


さらに、 t^0 = 0^0 = 0! = 1 , t \in \mathbb{R}から、

\displaystyle L = \frac{ 100! }{95!5!} (1-\theta)^{95} \theta^{5} \times \frac{ 20! }{1!19!} \theta (0.99-\theta)^{19}

と簡約化できる。


従って、\thetaの最尤推定値を \displaystyle \frac{\partial}{\partial \theta} \log L = 0 な θで導出できると信ずれば*2、

\displaystyle \frac{ \partial } {\partial \theta } \log L = 0 から、

\displaystyle \frac{ \partial } {\partial \theta } \log L = \frac{ \partial } {\partial \theta } \Bigl( \log(100!) - \log(95!) - \log(5!) + 95\log(1-\theta) + 5\log(\theta) + \log(20!) - \log(1!) - \log(19!) + \log(\theta) + 19\log(0.99 - \theta) \Bigr) = 0 \\\\ \displaystyle \iff 95 \frac{-1}{1-\theta} + 6 \frac{1}{\theta} + 19\frac{-1}{0.99 - \theta}= 0 \\\\ \displaystyle \iff 120\theta^2 -124.99\theta + 5.94 = 0 \\\\ \displaystyle \iff \theta = 0.991667 \ or \ 0.0499159

ここで、\phi + \theta \le 1 \iff 0.01 + \theta \le 1 \iff \theta \le 0.99 から、 \theta = 0.0499159 \simeq 0.05

となる。

[2]

チャップマン–コルモゴロフ方程式 より、推移確率行列Mのn乗はn回の推移の確率に等しいので、

  • M^nを計算し
  • 格付けA → 格付けCに対応するM^n上の成分すなわち
  • M^nの1行3列目の成分を求め

れば良い。さて、

\begin{equation}U^{T}MU = \begin{pmatrix} \lambda_{1} & 0 & 0 \\\\ 0 & \lambda_{2} & 0 \\\\ 0 & 0 & \lambda_{3} \end{pmatrix} \end{equation}

の両辺をn乗すると、

\begin{equation}U^{T}M^nU = \begin{pmatrix} \lambda_{1}^n & 0 & 0 \\\\ 0 & \lambda_{2}^n & 0 \\\\ 0 & 0 & \lambda_{3}^n \end{pmatrix} \end{equation}

となるので、

\begin{equation} M^n = U \begin{pmatrix} \lambda_{1}^n & 0 & 0 \\\\ 0 & \lambda_{2}^n & 0 \\\\ 0 & 0 & \lambda_{3}^n \end{pmatrix} \end{equation} U^T

従って、

\begin{equation} M^n = \begin{pmatrix} u_{11} & u_{12} & u_{13} \\\\ u_{21} & u_{22} & u_{23} \\\\ u_{31} & u_{32} & u_{33} \end{pmatrix} \begin{pmatrix} \lambda_{1}^n & 0 & 0 \\\\ 0 & \lambda_{2}^n & 0 \\\\ 0 & 0 & \lambda_{3}^n \end{pmatrix} \end{equation} \begin{pmatrix} u_{11} & u_{12} & u_{13} \\\\ u_{21} & u_{22} & u_{23} \\\\ u_{31} & u_{32} & u_{33} \end{pmatrix} ^T

\iff \begin{equation} M^n = \begin{pmatrix} u_{11} & u_{12} & u_{13} \\\\ u_{21} & u_{22} & u_{23} \\\\ u_{31} & u_{32} & u_{33} \end{pmatrix} \begin{pmatrix} \lambda_{1}^n & 0 & 0 \\\\ 0 & \lambda_{2}^n & 0 \\\\ 0 & 0 & \lambda_{3}^n \end{pmatrix} \end{equation} \begin{pmatrix} u_{11} & u_{21} & u_{31} \\\\ u_{12} & u_{22} & u_{32} \\\\ u_{13} & u_{23} & u_{33} \end{pmatrix}

となるので、M^nの1行3列目の成分は、

\begin{pmatrix} \lambda_{1}^n u_{11} & \lambda_{2}^n u_{12} & \lambda_{3}^n u_{13} \end{pmatrix} \begin{pmatrix} u_{31} & u_{32} & u_{33} \end{pmatrix}^T \\\\ = \displaystyle \lambda_{1}^n u_{11}u_{31} + \lambda_{2}^n u_{12}u_{32} + \lambda_{3}^n u_{13}u_{33} \\\\ = \displaystyle \sum_{k=1}^{3} \lambda_{k}^n u_{1k}u_{3k}


である。

*1:ここで尤度関数の変数が(θ,φ)からθのみになるのだと思われる。慈悲に感謝。

*2:真面目にやる場合はラグランジュの未定なんちゃら法とか極値が極大値になっているかとかを調べる必要があるゆえ。然し乍らどうやら信ずるものは救われるらしく、たとえば多項分布の推定 - MOXBOXを参照。

【一年ぶり】自宅のインターネットが使えなくなって使えるようになるまでの顛末

メモ

タイトルの通りですがまさか一年前と同じタイミングで同じ理由で回線が故障するとは笑 来年も起こるのだろうか🤔

去年はこちら↓ axjack.hatenablog.jp

要約

  • ネットが繋がらない
  • 去年と同じか！？
  • 回線事業者に連絡 → 局で故障があった

時系列

いつ だれ・なに どうした・どうなった
7/20 19:00 私 自宅のwifiが繋がらないと認知
同日 同時間帯 私 ルーターの落としあげ → 状況変わらず
同日 同時間帯 私 モデムの落としあげ → 状況変わらず
同日 同時間帯 私 ルーターの管理コンソール確認
同日 同時間帯 管理コンソール PPPoEサーバーが見つかりませんでした的なメッセージを表示
同日 同時間帯 私 去年の今頃もこんなことがあったなと思い出す
同日 同時間帯 私 ブログや日記を読み返し、プロパイダではなく回線事業者に連絡しようと決める
同日 20:00 私 回線事業者に電話 → メッセージ録音？にて伝言を残す
同日 21:30 回線事業者 私宛に折り返し連絡をする
同日 21:30 回線事業者 復旧した、とのこと
同日 21:32 私 回線復旧を確認

感想

誕生日前の祝砲なのかもしれない。

2019年6月 統計検定準一級 問3の[1]の(1)(2)

復習 統計

問3の[1]の(1)(2)

問3の[1]の(1)

母比率をpとする。また、\hat{p}は近似的に正規分布に従う。 n = 475、帰無仮説H_0:p=0.05、対立仮説H_1:p>0.05の片側検定。帰無仮説のもとで\hat{p}が0.0733以上となる確率は？

解答

帰無仮説のもと、\displaystyle{ P(z \ge \frac{\hat{p} - p}{\sqrt{ \frac{p(1-p)}{n}} } } ) を計算すれば良い。数字を代入すると、\displaystyle{ P ( z \ge \frac {0.0733 - 0.05} {\sqrt{ \frac{0.05(1-0.05)}{475} }} ) = P(z \ge 2.33) = 0.0099 \simeq 0.01}

問3の[1]の(2)

母比率をpとする。また、\hat{p}は近似的に正規分布に従う。 帰無仮説H_0:p=0.05、対立仮説H_1:p=0.1、有意水準2.5%の片側検定。検出力が90%となるような例数nは？

解答

帰無仮説のもとで有意水準\alpha = 0.025より、\displaystyle{ P( z_0 \ge \frac{ \hat{p} -0.05 } {\sqrt{ \frac{0.05(1-0.05)}{n} }} ) = 0.025}

また、対立仮説のもとで検出力1-\beta = 0.9 \iff \beta = 0.1 より、\displaystyle{ P( z_1 \le \frac{ \hat{p}-0.1} {\sqrt{ \frac{0.1(1-0.1)}{n} }} ) = 0.1 }

となるので、

\displaystyle{ \hat{p} = 0.05 + 1.96\sqrt{\frac{0.05(1-0.05) }{n} } }

\displaystyle{ \hat{p} = 0.1 - 1.28\sqrt{\frac{0.1(1-0.1) }{n} } }

をnについて解けば良い。これを解くと、n=263.2000\simeq264

重回帰分析をRで

R 勉強 統計

やること

永田『多変量解析法入門』(以下参考書)よりp.2のデータをもとに重回帰分析を行う。

ソースコード

# データ入力 #### 
hirosa <- c(51,38,57,51,53,77,63,69,72,73)
tiku   <- c(16,4,16,11,4,22,5,5,2,1)
kakaku <- c(3,3.2,3.3,3.9,4.4,4.5,4.5,5.4,5.4,6)

# データフレーム #### 
d <- data.frame(
  hirosa
  ,tiku
  ,kakaku
)

# 重回帰式 #### 
d.lm <- lm(kakaku ~ ., data = d)

# 要約 ####
summary(d.lm)

# 係数のみ表示 ####
print(d.lm)

# 新しいデータが与えられた時の予測値 #### 
# 新しいデータをデータフレームで用意し、
givenData <- data.frame(hirosa=70,tiku=10)

# 予測区間を出す
predict(d.lm,newdata=givenData,interval = "predict")

結果の確認

(1)回帰式

以下の通り参考書と一致。

> print(d.lm)

Call:
lm(formula = kakaku ~ ., data = d)

Coefficients:
(Intercept)       hirosa         tiku  
    1.02013      0.06680     -0.08083

(2)自由度調整済み寄与率

Adjusted R-squared: 0.9336 となった。

> summary(d.lm)

Call:
lm(formula = kakaku ~ ., data = d)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.32468 -0.20952  0.03939  0.17150  0.36196 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.020130   0.443624   2.300 0.055029 .  
hirosa       0.066805   0.007065   9.456 3.09e-05 ***
tiku        -0.080830   0.012241  -6.603 0.000303 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2636 on 7 degrees of freedom
Multiple R-squared:  0.9484,    Adjusted R-squared:  0.9336 
F-statistic:  64.3 on 2 and 7 DF,  p-value: 3.126e-05

(3)同じ地区で広さ=70平米, 築年数=10年, 価格=5.8千万円の提示は妥当か

係数を使って線形式に与えられたデータを代入し価格の予測値を出しても良い。

> coef(d.lm)
(Intercept)      hirosa        tiku 
 1.02012955  0.06680477 -0.08082993 

> sum(coef(d.lm) * c(1,70,10) )
[1] 4.888164

が、predict関数を用いてみると、

# 新しいデータをデータフレームで用意し、
givenData <- data.frame(hirosa=70,tiku=10)

> # 予測区間を出す
> predict(d.lm,newdata=givenData,interval = "predict")
       fit      lwr      upr
1 4.888164 4.214119 5.562209

と、予測値と予測区間が出るので便利。参考書と値が一致していることが確認できた。

2019年6月 統計検定準一級 問1

復習

はじめに

本番で解けなかった問題を解いてみます。今回は問１です。この問題で問われていることは

  • 確率分布の和
  • 条件付き確率分布

です。似たような問題ないかなぁと調べてみるとなんと、アクチュアリーの昭和39年数学1の問３にほぼ同じような問題があったので、これを見つつ今回の問題を解いてみることにしました。

問題を解く

以下、

  • λ1 : 3
  • λ2: 2
  • Z : 4

を代入すると記述1〜記述4の解となります。

ポアソン分布の性質

ポアソン分布P(X = k ; {\lambda}) = exp(-{\lambda}) \Big( \frac{ {\lambda}^k }{k!} \Big) は、

  • 平均 : λ
  • 分散 : λ

です。

ポアソン分布に従う確率変数の和の分布

P(X = k ; \lambda_1), P(Y = k ; {\lambda}_2)の時、P(X + Y = Z )が従う分布を求めます。

(はてなのmathjax記法がエラるので画像にて。。)

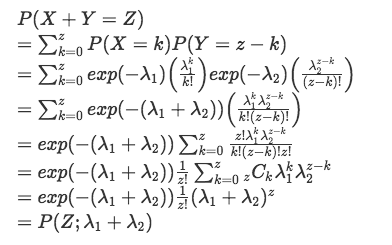
となるので、

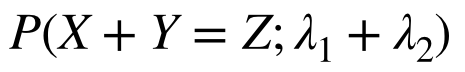
が和の分布となる(ポアソン分布の再生性が確認できた)。よって、和の分布は

  • 平均 : λ1 + λ2
  • 分散 : λ1 + λ2

となる。

条件付き確率分布

求めるのは、

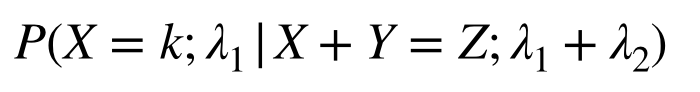
という確率分布である。計算すると、

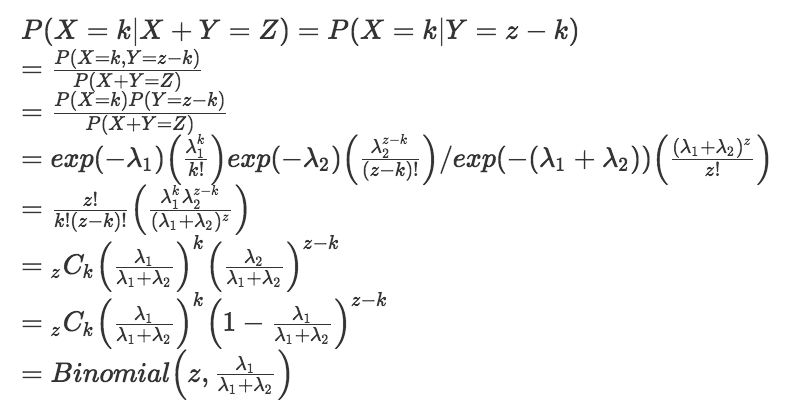
となるので、この条件付き確率分布は二項分布となる。

したがって、平均値は

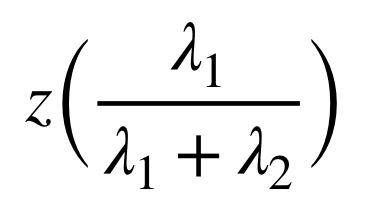
となる。

2019年6月 統計検定準一級 問10

復習

Rでロジスティック回帰

テーマはロジスティック回帰。問題文に記載された出典を調べると、Risk Analysis of the Space Shuttle: Pre-Challenger Prediction of Failureがヒットするので、このデータを用いれば再現が出来る(のだろうか)。ひとまずやってみると、

データの読み込み

# Field Erosion or blowby ####
yF <- c(0,1,0,0,0,0,0,0,1,1,1,0,0,2,0,0,0,0,0,0,1,0,1)
TD <- ifelse(yF > 0, 1, 0)
Temperature <- c(66,70,69,68,67,72,73,70,57,64,70,78,67,53,67,75,70,81,76,79,75,76,58)
r <- glm(TD ~ Temperature, family = binomial(link = logit))

結果

> summary(r)

Call:
glm(formula = TD ~ Temperature, family = binomial(link = logit))

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.0665  -0.7679  -0.3844   0.4541   2.2047  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)  
(Intercept)  14.9246     7.4235   2.010   0.0444 *
Temperature  -0.2302     0.1087  -2.117   0.0343 *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 28.267  on 22  degrees of freedom
Residual deviance: 20.511  on 21  degrees of freedom
AIC: 24.511

Number of Fisher Scoring iterations: 5

やや違うがおおよそ問題文の出力結果と合致している。

作図

plot(Temperature, TD)
points( Temperature,fitted(r), col='red')

問10の小問を解く

[1][2]

y_i は 互いに独立な確率変数Y_i の実現値であり、Y_i は (ア) に従う。
π_i( 0 < π_i < 1 ) について、構造式(イ) を仮定する。

とある。ロジスティック回帰なのでY_iはポアソン分布に従い、構造式(リンク関数？)はロジットなのでlog( (π_i / ( 1 - π_i) ) =である。

[3]

0 = 15.0429 - 0.2322 x_i をx_i について解くと、x_i = 64.78423772

[4]

確率を求めるのでロジットではなくロジスティック関数に戻して解いてみる。すると、π_i = 1 / ( 1 - exp( - (15.0429 - 0.2322x_i) ) ) で x_i <- 31 としてπ_iを求めれば良い。結局、

> 1/(1+exp(-7.8447))
[1] 0.9996083

となる。

終わりに

試験㆗、「聞いたことあるけど自分で解いたことないんだよなぁ、でも解けたら応用範囲が広そうだなぁ」と思っていた問題の１つ。

2019年6月度 統計検定準一級受験記録

陳述

記録

  • 受験日：2019/6/16(日)
  • 会場：中央大学 後楽園キャンパス

感想

  • 人生で一番難しい数学の試験だった
  • 手ごたえは皆無
  • 開始の合図とともに終了の合図が聞こえる
  • 試合開始直後に殺されていたがゾンビとして生きている気分(統計学的ゾンビ)
  • 分からなさすぎて「アハハ」って脳内から聞こえた(アハ体験?)
  • 1時間で退室
  • 年齢層は20代後半、ぱっと見社会人かなぁという人が多かった
  • 論述問題は大学の期末試験でよく見る横罫線な解答欄だった
  • 解けない問題・理解の浅い知識が分かった、という点では大変有意義な試験
  • (解けなかったものの)良い問題が多い
  • 試験開始前に勉強してる人が、2級の時より遥かに多かった

次回も受験しますか？

受験します。

反省点・改善すべき点

  • 基礎知識の深い理解をしよう
  • 統計検定なので統計と確率、とにかくこれに尽きる
    • 前回は機械学習寄りだった気もするが今回はTHE 統計というラインナップ
    • しっかり統計勉強しろよ？というメッセージ、か?
  • 「この分析方法見たことある」レベルで受験してしまったので、この手のモヤリティを失くすことが合格に繋がる気がした
  • インプットは知識の定着に結びつかない see アウトプット大全
    • とはいえアウトプット(=問題を解く)が容易に出来る範囲ではないというもどかしさ
    • しかし半年の勉強と今回の受験にて、真面目に真っ向からしっかり勉強するしかないことがわかった(大きな収穫)
    • 昔から言われているように、定義・定理・証明・理論・アルゴリズム・実装を大事にしよう

おわりに

ということでまた一年間みっちり勉強しようと思う所存です。とはいえずっと勉強だとアレなので、適宜Rを用いながらenjoyしようかとも思います。

初期値1から始めたニュートン法による平方根の近似値計算は、７回ほど反復計算しておけば大丈夫そうです。　

R 調べ物

はじめに

今日で令和元年ゴールデンウィークも無事終了です。

前回に引き続きニュートン法で平方根を求めてみました。今回は、N = [1,1000] の範囲でニュートン法を用いて10回反復近似計算する時、真の値と近似値との残差はどんな感じになるのか、を調べてみます。

全てのNに対して初期値１から始めると、Nが大きくなればなるほど収束が遅れるような気配もありますが、まぁそこは部屋の片隅に置いておきましょう。

ニュートン法による平方根の近似

aの平方根を求めるには、初期値x_0を設定し、

\displaystyle x_{n+1} \leftarrow x_n - \frac{ x_n^{2} - a }{ 2 x_n}

を順次反復計算します。今回はx_0 = 1とおきました。

例

a = 2, x_0 = 1の時、

\displaystyle x_{1} \leftarrow (1) - \frac{ ( 1 ) ^{2} - 2 }{ 2 \times ( 1 )} = 1.5

\displaystyle x_{2} \leftarrow (1.5) - \frac{ ( 1.5 ) ^{2} - 2 }{ 2 \times ( 1.5 )} = 1.416666667

\displaystyle x_{3} \leftarrow (1.416666667) - \frac{ ( 1.416666667 ) ^{2} - 2 }{ 2 \times ( 1.416666667 )} = 1.4142158687

\displaystyle x_{4} \leftarrow (1.4142158687) - \frac{ ( 1.4142158687 ) ^{2} - 2 }{ 2 \times ( 1.4142158687 )} = 1.414213563

結論

初期値が1であっても、７回ほど反復計算しておけば問題なさそう。

コード

#rm(list=ls())

# f(x) = x^2 - a をニュートン法で求める更新式
fnewton <- function(xn=1,a=2){
  return ( xn - ( xn^2 - a )/( 2 * xn ) )
}

# 初期化
how_many_times_rep <- 10
N <- 1000
xs <- 1:N
root_xs <- sqrt(xs)
zeros <- rep(0,length(xs))

# 結果格納用行列
mat.x <- cbind( 
  matrix(c( xs,root_xs ),nrow = length(xs))
  ,matrix( rep(zeros, how_many_times_rep), nrow = length(zeros))
)

mat.x[,3] <- fnewton(xn = 1, a = mat.x[,1])

# ニュートン法にて更新
for(i in 4:(how_many_times_rep+2) ){
  mat.x[,i] = fnewton(xn = mat.x[,i-1], a = mat.x[,1])
}

#mat.dif <- matrix(0, nrow = nrow(mat.x), ncol = ncol(mat.x))
mat.dif <- mat.x

# 真の値 - 近似値
for(i in 3:(how_many_times_rep+2)){
  mat.dif[,i] <- mat.x[,2] - mat.x[,i]
}

# 結果確認
summary(mat.dif[,-c(1,2)])

par(family="Osaka")
boxplot(mat.dif[,-c(1,2)],
        col="lightpink",
        names=paste0(1:how_many_times_rep,"回目"),
        las=2,
        main=paste0("真の値と近似値との残差の箱ひげ図(N = 1 ~ ",N,")")
)

結果確認

要約統計量

summary の値を書き出すと、

V1               V2               V3               V4                V5         
 Min.   :-468.9   Min.   :-219.6   Min.   :-95.99   Min.   :-36.103   Min.   :-9.6226  
 1st Qu.:-348.2   1st Qu.:-161.4   1st Qu.:-69.00   1st Qu.:-24.697   1st Qu.:-5.8550  
 Median :-228.4   Median :-104.0   Median :-42.79   Median :-14.052   Median :-2.7105  
 Mean   :-229.7   Mean   :-105.3   Mean   :-44.04   Mean   :-15.158   Mean   :-3.3997  
 3rd Qu.:-110.0   3rd Qu.: -48.1   3rd Qu.:-18.09   3rd Qu.: -4.824   3rd Qu.:-0.5632  
 Max.   :   0.0   Max.   :   0.0   Max.   :  0.00   Max.   :  0.000   Max.   : 0.0000  

       V6                  V7                   V8                   V9            
 Min.   :-1.122493   Min.   :-1.924e-02   Min.   :-5.849e-06   Min.   :-5.400e-13  
 1st Qu.:-0.515571   1st Qu.:-4.763e-03   1st Qu.:-4.140e-07   1st Qu.:-3.553e-15  
 Median :-0.146451   Median :-4.762e-04   Median :-5.069e-09   Median : 0.000e+00  
 Mean   :-0.293577   Mean   :-3.268e-03   Mean   :-5.871e-07   Mean   :-3.005e-14  
 3rd Qu.:-0.009673   3rd Qu.:-2.953e-06   3rd Qu.: 0.000e+00   3rd Qu.: 0.000e+00  
 Max.   : 0.000000   Max.   : 0.000e+00   Max.   : 0.000e+00   Max.   : 3.553e-15  
      V10            
 Min.   :-3.553e-15  
 1st Qu.: 0.000e+00  
 Median : 0.000e+00  
 Mean   : 3.242e-17  
 3rd Qu.: 0.000e+00  
 Max.   : 3.553e-15

でした。

  • V6列(6回目の反復)で残差の絶対値の最小値がほぼ1
  • 7回目で　　〃　　ほぼほぼ0

ですね。7回電卓ぽちぽちすれば平方根が得られそうです。

箱ひげ図

f:id:axjack:20190506230038p:plain

残差の範囲は反復回数が増す毎にどんどん小さくなっていきますね。５回目あたりで箱が見えなくなり、６回目あたりでヒゲもぺっちゃんこに見えます。

おわりに

計算方法覚えておけばルート機能要らない気もしないでも無いですね。脳内記憶容量を節約するならやはりルート付き電卓を買いましょう。

axjack is said to be an abbreviation for An eXistent JApanese Cool Klutz.