axjack's blog

### axjack is said to be an abbreviation for An eXistent JApanese Cool Klutz ###

とりあえずアソシエーション分析する〜その３〜

調べ物 統計

手を動かして形は理解したっぽいので、今度こそ(？)仕組みを理解する編です。いきなり読むと分からなくなるので、何となくアソシエーション分析のパッケージ{arules}は動かせたけどイマイチ意味がわからないんだよなーという状態になった時に読むのをお勧めします。


前回↓
axjack.hatenablog.jp

もくじ

アソシエーション分析の内部で使っているデータはどんな形式なのか？

アソシエーション分析の内部で使っているデータとは、{arules}のread.transactions関数で読み込んだものを指しています。この読み込んだデータをSQLで喩えてみるべく、TransというSQLのテーブルにアソシエーション分析の内部で使っているデータが入っているとします。関係スキーマ表記とcreate table 表記を用いてTransテーブルを表すと、以下のようになります。なおここで、アイテムが全部でp種類あるとしましょう。

関係スキーマ表記

Trans( tranID, item_1, item_2, ..., item_p )
となります。下線部は主キーです。

create table 表記

create table Trans(
    tranID nvarchar(max) not null primary key
  , item_1  bit not null
  , item_2 bit not null
  , ...
  , item_p bit not null
);

となります。

記号Mと演算子σを定義する

ここで唐突ですが、記号Mと演算子σをSQLを用いて定義します。
なお、記号「:=」は「左辺を右辺で定義する」、記号「=」は「左辺と右辺は等しい・上の式と右の式は等しい」と解釈してください。

記号M は Transの全行数

記号M は Transの全行数を表します。select文で書くと、

M := select count(*) from Trans;

となります。

演算子σ は Transの抽出条件つきの行数

幾つか例示します。ここでXやYはTransテーブルにあるtranIDではない任意の列(すなわちitem_1〜item_pのどれか)とします。

カッコの中が１つの場合

σ( X ) := select count(*) from Trans where X = 1;

カッコの中が２つの場合

σ( X∪Y ) := select count(*) from Trans where X = 1 and Y = 1;

σ( Y∪X ) := select count(*) from Trans where Y = 1 and X = 1;
= select count(*) from Trans where X = 1 and Y = 1;
= σ( X∪Y )

Xが複合アイテム( X = {X1, X2} )のような場合は、

σ( X ) = σ( {X1, X2} ) := select count(*) from Trans where X1 = 1 and X2 = 1;

となります。*1

相関ルールの３指標は何者なのか？

相関ルールの３指標とは、

  • Support(サポート; 支持度)
  • Confidence(コンフィデンス; 確信度)
  • Lift(リフト; リフト値)

を指します。

さて以下にて、σはSupport・Confidence・ Liftを用いて表せることを示します。

Support(サポート; 支持度)

Suppと略します。

Supp( X ) := σ(X) / M
より、σ(X) = Supp( X ) * M

Supp( X ⇒ Y ) := σ( X∪Y ) / M
より、σ( X∪Y ) = Supp( X ⇒ Y ) * M

ということで、SuppにMを掛けると「ルールが含まれるトランザクション数」を取り出せます。

Confidence(コンフィデンス; 確信度)

Confと略します。

Conf( X ⇒ Y ) := Supp( X ⇒ Y ) / Supp( X ) 
より、Supp( X ) = Supp( X ⇒ Y )/Conf( X ⇒ Y )
ところでSupp( X ) = σ( X ) / Mなので
σ( X ) = ( Supp( X ⇒ Y )/Conf( X ⇒ Y ) ) * M

ということで、SuppをConfで割ってからMを掛けると
「ルールの前件(X ⇒ YにおけるXの部分)が含まれるトランザクション数」が取り出せます。

Lift(リフト; リフト値)

Lift( X ⇒ Y ) := Conf( X ⇒ Y ) / Supp(Y) 
より、Supp( Y ) = Conf( X ⇒ Y )/Lift( X ⇒ Y )
ところでSupp( Y ) = σ( Y ) / Mなので
σ( Y ) = ( Conf( X ⇒ Y )/Lift( X ⇒ Y ) ) * M

ということで、ConfをLiftで割ってからMを掛けると
「ルールの後件(X ⇒ YにおけるYの部分)が含まれるトランザクション数」が取り出せます。


以上をまとめると、

σ Supp,Conf,Lift で表すと
σ( X∪Y ) Supp( X ⇒ Y ) * M
σ( X ) ( Supp( X ⇒ Y )/Conf( X ⇒ Y ) ) * M
σ( Y ) ( Conf( X ⇒ Y )/Lift( X ⇒ Y ) ) * M

となります。

これの何が嬉しいかというと、アソシエーション分析で得られたSupp・Conf・Liftの値を割り算掛け算することによって比率から個数に変換することができるわけです。(なぜならば「演算子σ は Transの抽出条件つきの行数」であるから、です。)

実際のデータで確かめてみる

アソシエーション分析(1)から表を２つ引用します。

表：トランザクション
f:id:axjack:20190806211933p:plain

表：アソシエーション分析の結果
f:id:axjack:20190806211949p:plain

いくつかのルールにてσを求めてみます。ここでM = 5とします。

例１

ルール lhs ⇒ rhs supp conf lift
6 ソーセージ ⇒ オムツ 0.2 1 1.66

は

σ( ソーセージ∪オムツ ) = supp * M = 0.2 * 5 = 1
σ( ソーセージ ) = (supp/conf) * M = (0.2/1) * 5 = 1
σ( オムツ ) = (conf/lift) * M = (1/1.666) * 5 = 3

となります。

例２

ルール lhs ⇒ rhs supp conf lift
11 タバコ ⇒ 弁当 0.2 1 2.5

は

σ( タバコ∪弁当 ) = supp * M = 0.2 * 5 = 1
σ( ソーセージ ) = (supp/conf) * M = (0.2/1) * 5 = 1
σ( オムツ ) = (conf/lift) * M = (1/2.5) * 5 = 2

となります。

例３

ルール lhs ⇒ rhs supp conf lift
17 {オムツ, ソーセージ } ⇒ ビール 0.2 1 1.25

は

σ( {オムツ, ソーセージ}∪{ビール} ) = supp * M = 0.2 * 5 = 1
σ( {オムツ, ソーセージ} ) = (supp/conf) * M = (0.2/1) * 5 = 1
σ( {ビール} ) = (conf/lift) * M = (1/1.25) * 5 = 4

となります。

おわりに

アソシエーション分析{arules}をいじって一週間ぐらい経過しました。支持度・確信度・リフト値の意味がわからずムムムとなっていた状態からはだいぶ進歩したような気持ちです。比率を個数に直すと結構「なるほど！」と思えてきました。

「アソシエーション分析してみたけど、比率だけだと実感が湧かない！」という人は比率を個数に直して考えると理解が深まるかもしれません。また、個数に直してみると「比率はどうなってるの？」とやっぱり比率が恋しく？なりますね笑　

こんなかんじで比率・個数を行き来していくとアソシエーション分析の面白さがより一層分かってくるのかなぁ、と感じました。

参考

en.wikipedia.org

www.cis.doshisha.ac.jp

*1:Association rule learning - Wikipediaによると、"Note that supp(X∪Y) means the support of the union of the items in X and Y. This is somewhat confusing since we normally think in terms of probabilities of events and not sets of items. " と書かれている。一見「∪」の記号からORを連想してしまうが決してそうではないということを注として書いておく。X∪Yに於けるXは集合でありYも集合である。すなわちX = {みかん,ビール}, Y = {ビール, おむつ} ならば X∪Y = {みかん, ビール, おむつ}である。(※ X∩Y は {ビール} なことに注意。) そして結果的にσ( X∪Y )をselect count(*)文に翻訳するとそれぞれのアイテムをbit型な列とした時に「=1」でandを使って結んだ抽出条件と同じになる。この場合はσ( X∪Y ) = select count(*) from Trans where みかん = 1 and ビール = 1 and おむつ = 1である。集合の要素と列で同じ名前を使っていることが混乱の原因なのかもしれないものの、そこは上手くLet's 脳内変換。

とりあえずアソシエーション分析する〜その２〜

前回に引き続きとりアソしてみます。

前回↓ axjack.hatenablog.jp

tranID で group-by した時グループに属するitemが1個のもの、を除外する

ファイルの準備

dat_singleをコピってitemが1つしかないtranIDの行を作成する。

axjack:dat $ diff dat_single.csv dat_single.v2.csv
35a36,41
> 11,ビール
> 12,ビール
> 13,ビール
> 14,ワイン
> 15,ワイン
> 16,ワイン

前処理

アソシエーション分析用のファイルはCSVから読み込むと良い、とのことなのでファイル読み込み→加工→ファイル書き出し→再度読み込みします。

# load library ####
library(dplyr)
library(readr)

# single形式のCSVファイルを読み込む
mytemp <- read_csv(file="dat/dat_single.v2.csv"
                ,col_types = c("cc")
                ,col_names = c("tranID","item")
                ,quote = '\"'
                #,skip = 1 #ヘッダがある場合は1行目をスキップする
                )

# transactionの長さ1ではないものを抽出し
mytemp %>% unique() %>% group_by(tranID) %>% filter( n() != 1 ) -> mytemp.f

# ファイルに書き出す
write_csv(mytemp.f,path="dat/dat_single.f.csv", col_names = FALSE)

末尾の６行が消えたか確認すると、

> tail(mytemp,   n=6)
# A tibble: 6 x 2
  tranID item  
  <chr>  <chr> 
1 11     ビール
2 12     ビール
3 13     ビール
4 14     ワイン
5 15     ワイン
6 16     ワイン
> tail(mytemp.f, n=6)
# A tibble: 6 x 2
# Groups:   tranID [3]
  tranID item      
  <chr>  <chr>     
1 8      チーズ    
2 9      ワイン    
3 9      牛肉      
4 9      じゃがいも
5 10     ワイン    
6 10     こんにゃく

消えました。ではCSVファイルをread.transactionsで読み込みます。

データの確認

###########################
# アソシエーション分析 ####
###########################
# load library #### 
library(arules)

# load CSV ####
# (1)元データ
ds <- read.transactions(
  file = "dat/dat_single.csv"
  , format = "single"
  , sep = ","
  , cols = c(1,2)
  , rm.duplicates = T
#  , skip = 1
)

# (2)レコード追加したデータ
dsv2 <- read.transactions(
  file = "dat/dat_single.v2.csv"
  , format = "single"
  , sep = ","
  , cols = c(1,2)
  , rm.duplicates = T
  #  , skip = 1
)

# (3) "(2)"からlength=1のtransactionを削除したデータ
dsf <- read.transactions(
  file = "dat/dat_single.f.csv"
  , format = "single"
  , sep = ","
  , cols = c(1,2)
  , rm.duplicates = T
  #  , skip = 1
)

トランザクションの行数列数を確認すると

> ds
transactions in sparse format with
 10 transactions (rows) and
 19 items (columns)
> dsv2
transactions in sparse format with
 16 transactions (rows) and
 19 items (columns)
> dsf
transactions in sparse format with
 10 transactions (rows) and
 19 items (columns)

たしかにdsv2は6トランザクション消すことに成功しています。summaryをみて見ると、

> summary(ds)
transactions as itemMatrix in sparse format with
 10 rows (elements/itemsets/transactions) and
 19 columns (items) and a density of 0.1842105 

most frequent items:
ソーセージ     ビール     ワイン       牛肉     生野菜    (Other) 
         3          3          3          3          3         20 

element (itemset/transaction) length distribution:
sizes
2 3 4 5 
1 4 4 1 

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
    2.0     3.0     3.5     3.5     4.0     5.0 
> summary(dsv2)
transactions as itemMatrix in sparse format with
 16 rows (elements/itemsets/transactions) and
 19 columns (items) and a density of 0.1348684 

most frequent items:
    ビール     ワイン ソーセージ       牛肉     生野菜    (Other) 
         6          6          3          3          3         20 

element (itemset/transaction) length distribution:
sizes
1 2 3 4 5 
6 1 4 4 1 

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  1.000   1.000   3.000   2.562   4.000   5.000

よい感じです。あとはaprioriに作ったtransactionを食わせればアソシエーション分析の完成かと。ここから先は前回と同じなので省略。

参考

とりあえずアソシエーション分析する

調べ物 統計

タイトル通りです。とりあえず動かしてみたい！という願望でやってみました。理解は後からついてくると信じて、まずは手を動かしたいという人向け？の記事です。

読み込むデータの準備

前処理なしのトランザクションデータを{arules}パッケージで読み込む方法 - 六本木で働くデータサイエンティストのブログ にあるデータに１行追加したものを利用します。gistにアップロードしました。

ところでどうやら、CSVの最終行に空行が無いと読み込みエラーになるっぽい？ので、エラーが出たら空行付け足してみてください。

dat_basket.csvはbasket形式のデータで、dat_single.csvは同データをsingle形式にしたものです。

gist.github.com

データの読み込み

read.transactionsの引数はどうなってるんじゃ？という人は?read.transactionsしてみましょう。冷静に読むと丁寧に説明が書かれております。

# load library #### 
library(arules)

# load CSV ####
# format = "basket" の場合
mytran_basket <- read.transactions(
  file = "dat/dat_basket.csv"
  , format = "basket"
  , sep = ","
  , cols = NULL
  , rm.duplicates = T
)

# format = "single" の場合
mytran_single <- read.transactions(
  file = "dat/dat_single.csv"
  , format = "single"
  , sep = ","
  , cols = c(1,2)
  , rm.duplicates = T
)

生成したtranデータの確認

mytran_basketもmytran_singleも同じ内容なので、mytran_basketを使います。

> mytran_basket
transactions in sparse format with
 10 transactions (rows) and
 19 items (columns)
> summary(mytran_basket)
transactions as itemMatrix in sparse format with
 10 rows (elements/itemsets/transactions) and
 19 columns (items) and a density of 0.1842105 

most frequent items:
    ビール ソーセージ     柿ピー       牛肉     生野菜    (Other) 
         4          3          3          3          3         19 

element (itemset/transaction) length distribution:
sizes
2 3 4 5 
1 4 4 1 

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
    2.0     3.0     3.5     3.5     4.0     5.0 

includes extended item information - examples:
      labels
1     アイス
2     おむつ
3 こんにゃく

適当にピックアップすると、

transactions in sparse format with
 10 transactions (rows) and
 19 items (columns)

transactionsは10件あり、品目数は19件と云うことがわかります。dat_basket.csvは10行だしdat_single.csvのtransaction-IDは10個なので確かにあってそうです。

most frequent items:
    ビール ソーセージ     柿ピー       牛肉     生野菜    (Other) 
         4          3          3          3          3         19

transactionに含まれる品目のうち、最も多いのはビールで次はソーセージで・・・と云うことがわかります。CSVの中を検索すると確かにあっています。

element (itemset/transaction) length distribution:
sizes
2 3 4 5 
1 4 4 1

transactionの長さとはtransactionに含まれる品目の数だそうで、長さ2と長さ5が1件で長さ3と長さ4が4件だと云うことがわかります。目視で確認すると確かにあっています。

というわけで、ここまでは読み込んだtransactionについての情報でした。

いよいよアソシエーション分析

流れは、apriori関数にデータを突っ込んでrulesを生成→inspectで中身を見る、です。

> mytran_basket.apr <- apriori(mytran_basket, parameter = NULL)
Apriori

Parameter specification:
 confidence minval smax arem  aval originalSupport maxtime support minlen maxlen target   ext
        0.8    0.1    1 none FALSE            TRUE       5     0.1      1     10  rules FALSE

Algorithmic control:
 filter tree heap memopt load sort verbose
    0.1 TRUE TRUE  FALSE TRUE    2    TRUE

Absolute minimum support count: 1 

set item appearances ...[0 item(s)] done [0.00s].
set transactions ...[19 item(s), 10 transaction(s)] done [0.00s].
sorting and recoding items ... [19 item(s)] done [0.00s].
creating transaction tree ... done [0.00s].
checking subsets of size 1 2 3 4 5 done [0.00s].
writing ... [136 rule(s)] done [0.00s].
creating S4 object  ... done [0.00s].

[136 rule(s)]ということで136の相関ルールが抽出されました。inspectしてみましょう。

> inspect( head(sort(mytran_basket.apr,by="support"),15) )
     lhs                    rhs            support confidence lift      count
[1]  {柿ピー}            => {ビール}       0.3     1           2.500000 3    
[2]  {じゃがいも}        => {牛肉}         0.2     1           3.333333 2    
[3]  {果物}              => {豆腐}         0.2     1           3.333333 2    
[4]  {果物}              => {生野菜}       0.2     1           3.333333 2    
[5]  {ソーセージ,柿ピー} => {ビール}       0.2     1           2.500000 2    
[6]  {ソーセージ,ビール} => {柿ピー}       0.2     1           3.333333 2    
[7]  {果物,豆腐}         => {生野菜}       0.2     1           3.333333 2    
[8]  {果物,生野菜}       => {豆腐}         0.2     1           3.333333 2    
[9]  {生野菜,豆腐}       => {果物}         0.2     1           5.000000 2    
[10] {チーズ}            => {ワイン}       0.1     1           5.000000 1    
[11] {チーズ}            => {ソーセージ}   0.1     1           3.333333 1    
[12] {おむつ}            => {ドレッシング} 0.1     1          10.000000 1    
[13] {ドレッシング}      => {おむつ}       0.1     1          10.000000 1    
[14] {おむつ}            => {ビール}       0.1     1           2.500000 1    
[15] {おむつ}            => {生野菜}       0.1     1           3.333333 1    
>

とりあえず一行目のこれ↓

     lhs                    rhs            support confidence lift      count
[1]  {柿ピー}            => {ビール}       0.3     1           2.500000 3

を解釈するには リフト値とは何？ Weblio辞書 を読むと良いです。すると、一行目は

  • support ： 全体の30%が柿ピーとビールを一緒に購入している。
  • confidence：柿ピー購入者の100%が柿ピーとビールを一緒に購入している。
  • lift：ビールをいきなり購入するよりも、柿ピーを買ってビールを購入する確率が2.5倍大きい。

と解釈できます。ちなみにcountの3をtransactions数の10で割るとsupportとなっています。

おわりに

とりあえず動かすことができたら、support(支持度)・confidence(確信度)・lift(リフト値)について調べて見ると良いかと思われます。自分もまさに調べているところですので参考URLをご参照あれ。併売率・購買率などの用語で調べてもだいたいアソシエーション分析についての記事が見つかるので併せてどうぞ。

参考

2019年6月 統計検定準一級 問11

復習

問題の超大雑把な概要

詳細はお手元に問題を用意してください。

定数の情報：

\theta,\phi \in [0,1], \phi + \theta \le 1

推移確率行列M：

\begin{equation}M=\begin{pmatrix} 1-\theta & \theta & 0 \\\\ \theta & 1-\theta-\phi & \phi \\\\ 0 & \phi & 1-\phi \end{pmatrix} \end{equation}

問題

[1]

格付けの状態(A,B,C)を番号(1,2,3)に対応させ、 i,j \in \{1,2,3\} とする。ある年の格付けAが100社・格付けBが20社・格付けCが0社。翌年において、
・A→Bに推移した企業が5社
・B→Aに推移した企業が1社
・他に変化はなかった
・\phi = 0.01とする

このとき、\thetaの最尤推定値を、小数点第3位を四捨五入して答えよ。

[2]

Mの固有値をλとし、直交行列(U)_{ij}= u_{ij}を
\begin{equation}U^{T}MU = \begin{pmatrix} \lambda_{1} & 0 & 0 \\\\ 0 & \lambda_{2} & 0 \\\\ 0 & 0 & \lambda_{3} \end{pmatrix} \end{equation}
を満たすように取る。
t年に於いて格付けAの企業がt+nにおいて格付けCである確率を、n・λ・uを用いて表せ。

解答

[1]

ある年→翌年の格付けの変化は、

\begin{pmatrix} 95 & 5 & 0 \\\\ 1 & 19 & 0 \\\\ 0 & 0 & 0 \end{pmatrix}

と表される。求めたいのはθの最尤推定値である。確率は与えられている。確率分布は３項の状態を扱っているので多項分布の３項版とする。


多項分布の式は、\displaystyle Mult( m | \mu, N ) = \frac{N!}{m_{1}! \cdots m_{K}! } \prod_{k=1}^{K}\mu_{k}^{m_k} ただし N=\sum_{k=1}^K m_k

よって、尤度関数Lは

\displaystyle L = \frac{ (95+5+0)! }{95!5!0!} (1-\theta)^{95} \theta^{5} 0^0 \times \frac{ (1+19+0)! }{1!19!0!} \theta^1 (1-\theta-\phi)^{19} \phi^0 \times \frac{ (0+0+0)! } {0!0!0!} 0^0 \phi^0 (1-\phi)^0


\phi = 0.01*1を代入しながら整理すると、

\displaystyle L = \frac{ (100)! }{95!5!0!} (1-\theta)^{95} \theta^{5} 0^0 \times \frac{ (20)! }{1!19!0!} \theta^1 (1-\theta-0.01)^{19} (0.01)^0 \times \frac{ (0+0+0)! } {0!0!0!} 0^0 (0.01)^0 (1-0.01)^0


さらに、 t^0 = 0^0 = 0! = 1 , t \in \mathbb{R}から、

\displaystyle L = \frac{ 100! }{95!5!} (1-\theta)^{95} \theta^{5} \times \frac{ 20! }{1!19!} \theta (0.99-\theta)^{19}

と簡約化できる。


従って、\thetaの最尤推定値を \displaystyle \frac{\partial}{\partial \theta} \log L = 0 な θで導出できると信ずれば*2、

\displaystyle \frac{ \partial } {\partial \theta } \log L = 0 から、

\displaystyle \frac{ \partial } {\partial \theta } \log L = \frac{ \partial } {\partial \theta } \Bigl( \log(100!) - \log(95!) - \log(5!) + 95\log(1-\theta) + 5\log(\theta) + \log(20!) - \log(1!) - \log(19!) + \log(\theta) + 19\log(0.99 - \theta) \Bigr) = 0 \\\\ \displaystyle \iff 95 \frac{-1}{1-\theta} + 6 \frac{1}{\theta} + 19\frac{-1}{0.99 - \theta}= 0 \\\\ \displaystyle \iff 120\theta^2 -124.99\theta + 5.94 = 0 \\\\ \displaystyle \iff \theta = 0.991667 \ or \ 0.0499159

ここで、\phi + \theta \le 1 \iff 0.01 + \theta \le 1 \iff \theta \le 0.99 から、 \theta = 0.0499159 \simeq 0.05

となる。

[2]

チャップマン–コルモゴロフ方程式 より、推移確率行列Mのn乗はn回の推移の確率に等しいので、

  • M^nを計算し
  • 格付けA → 格付けCに対応するM^n上の成分すなわち
  • M^nの1行3列目の成分を求め

れば良い。さて、

\begin{equation}U^{T}MU = \begin{pmatrix} \lambda_{1} & 0 & 0 \\\\ 0 & \lambda_{2} & 0 \\\\ 0 & 0 & \lambda_{3} \end{pmatrix} \end{equation}

の両辺をn乗すると、

\begin{equation}U^{T}M^nU = \begin{pmatrix} \lambda_{1}^n & 0 & 0 \\\\ 0 & \lambda_{2}^n & 0 \\\\ 0 & 0 & \lambda_{3}^n \end{pmatrix} \end{equation}

となるので、

\begin{equation} M^n = U \begin{pmatrix} \lambda_{1}^n & 0 & 0 \\\\ 0 & \lambda_{2}^n & 0 \\\\ 0 & 0 & \lambda_{3}^n \end{pmatrix} \end{equation} U^T

従って、

\begin{equation} M^n = \begin{pmatrix} u_{11} & u_{12} & u_{13} \\\\ u_{21} & u_{22} & u_{23} \\\\ u_{31} & u_{32} & u_{33} \end{pmatrix} \begin{pmatrix} \lambda_{1}^n & 0 & 0 \\\\ 0 & \lambda_{2}^n & 0 \\\\ 0 & 0 & \lambda_{3}^n \end{pmatrix} \end{equation} \begin{pmatrix} u_{11} & u_{12} & u_{13} \\\\ u_{21} & u_{22} & u_{23} \\\\ u_{31} & u_{32} & u_{33} \end{pmatrix} ^T

\iff \begin{equation} M^n = \begin{pmatrix} u_{11} & u_{12} & u_{13} \\\\ u_{21} & u_{22} & u_{23} \\\\ u_{31} & u_{32} & u_{33} \end{pmatrix} \begin{pmatrix} \lambda_{1}^n & 0 & 0 \\\\ 0 & \lambda_{2}^n & 0 \\\\ 0 & 0 & \lambda_{3}^n \end{pmatrix} \end{equation} \begin{pmatrix} u_{11} & u_{21} & u_{31} \\\\ u_{12} & u_{22} & u_{32} \\\\ u_{13} & u_{23} & u_{33} \end{pmatrix}

となるので、M^nの1行3列目の成分は、

\begin{pmatrix} \lambda_{1}^n u_{11} & \lambda_{2}^n u_{12} & \lambda_{3}^n u_{13} \end{pmatrix} \begin{pmatrix} u_{31} & u_{32} & u_{33} \end{pmatrix}^T \\\\ = \displaystyle \lambda_{1}^n u_{11}u_{31} + \lambda_{2}^n u_{12}u_{32} + \lambda_{3}^n u_{13}u_{33} \\\\ = \displaystyle \sum_{k=1}^{3} \lambda_{k}^n u_{1k}u_{3k}


である。

*1:ここで尤度関数の変数が(θ,φ)からθのみになるのだと思われる。慈悲に感謝。

*2:真面目にやる場合はラグランジュの未定なんちゃら法とか極値が極大値になっているかとかを調べる必要があるゆえ。然し乍らどうやら信ずるものは救われるらしく、たとえば多項分布の推定 - MOXBOXを参照。

【一年ぶり】自宅のインターネットが使えなくなって使えるようになるまでの顛末

メモ

タイトルの通りですがまさか一年前と同じタイミングで同じ理由で回線が故障するとは笑 来年も起こるのだろうか🤔

去年はこちら↓ axjack.hatenablog.jp

要約

  • ネットが繋がらない
  • 去年と同じか！？
  • 回線事業者に連絡 → 局で故障があった

時系列

いつ だれ・なに どうした・どうなった
7/20 19:00 私 自宅のwifiが繋がらないと認知
同日 同時間帯 私 ルーターの落としあげ → 状況変わらず
同日 同時間帯 私 モデムの落としあげ → 状況変わらず
同日 同時間帯 私 ルーターの管理コンソール確認
同日 同時間帯 管理コンソール PPPoEサーバーが見つかりませんでした的なメッセージを表示
同日 同時間帯 私 去年の今頃もこんなことがあったなと思い出す
同日 同時間帯 私 ブログや日記を読み返し、プロパイダではなく回線事業者に連絡しようと決める
同日 20:00 私 回線事業者に電話 → メッセージ録音？にて伝言を残す
同日 21:30 回線事業者 私宛に折り返し連絡をする
同日 21:30 回線事業者 復旧した、とのこと
同日 21:32 私 回線復旧を確認

感想

誕生日前の祝砲なのかもしれない。

2019年6月 統計検定準一級 問3の[1]の(1)(2)

復習 統計

問3の[1]の(1)(2)

問3の[1]の(1)

母比率をpとする。また、\hat{p}は近似的に正規分布に従う。 n = 475、帰無仮説H_0:p=0.05、対立仮説H_1:p>0.05の片側検定。帰無仮説のもとで\hat{p}が0.0733以上となる確率は？

解答

帰無仮説のもと、\displaystyle{ P(z \ge \frac{\hat{p} - p}{\sqrt{ \frac{p(1-p)}{n}} } } ) を計算すれば良い。数字を代入すると、\displaystyle{ P ( z \ge \frac {0.0733 - 0.05} {\sqrt{ \frac{0.05(1-0.05)}{475} }} ) = P(z \ge 2.33) = 0.0099 \simeq 0.01}

問3の[1]の(2)

母比率をpとする。また、\hat{p}は近似的に正規分布に従う。 帰無仮説H_0:p=0.05、対立仮説H_1:p=0.1、有意水準2.5%の片側検定。検出力が90%となるような例数nは？

解答

帰無仮説のもとで有意水準\alpha = 0.025より、\displaystyle{ P( z_0 \ge \frac{ \hat{p} -0.05 } {\sqrt{ \frac{0.05(1-0.05)}{n} }} ) = 0.025}

また、対立仮説のもとで検出力1-\beta = 0.9 \iff \beta = 0.1 より、\displaystyle{ P( z_1 \le \frac{ \hat{p}-0.1} {\sqrt{ \frac{0.1(1-0.1)}{n} }} ) = 0.1 }

となるので、

\displaystyle{ \hat{p} = 0.05 + 1.96\sqrt{\frac{0.05(1-0.05) }{n} } }

\displaystyle{ \hat{p} = 0.1 - 1.28\sqrt{\frac{0.1(1-0.1) }{n} } }

をnについて解けば良い。これを解くと、n=263.2000\simeq264

重回帰分析をRで

R 勉強 統計

やること

永田『多変量解析法入門』(以下参考書)よりp.2のデータをもとに重回帰分析を行う。

ソースコード

# データ入力 #### 
hirosa <- c(51,38,57,51,53,77,63,69,72,73)
tiku   <- c(16,4,16,11,4,22,5,5,2,1)
kakaku <- c(3,3.2,3.3,3.9,4.4,4.5,4.5,5.4,5.4,6)

# データフレーム #### 
d <- data.frame(
  hirosa
  ,tiku
  ,kakaku
)

# 重回帰式 #### 
d.lm <- lm(kakaku ~ ., data = d)

# 要約 ####
summary(d.lm)

# 係数のみ表示 ####
print(d.lm)

# 新しいデータが与えられた時の予測値 #### 
# 新しいデータをデータフレームで用意し、
givenData <- data.frame(hirosa=70,tiku=10)

# 予測区間を出す
predict(d.lm,newdata=givenData,interval = "predict")

結果の確認

(1)回帰式

以下の通り参考書と一致。

> print(d.lm)

Call:
lm(formula = kakaku ~ ., data = d)

Coefficients:
(Intercept)       hirosa         tiku  
    1.02013      0.06680     -0.08083

(2)自由度調整済み寄与率

Adjusted R-squared: 0.9336 となった。

> summary(d.lm)

Call:
lm(formula = kakaku ~ ., data = d)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.32468 -0.20952  0.03939  0.17150  0.36196 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.020130   0.443624   2.300 0.055029 .  
hirosa       0.066805   0.007065   9.456 3.09e-05 ***
tiku        -0.080830   0.012241  -6.603 0.000303 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2636 on 7 degrees of freedom
Multiple R-squared:  0.9484,    Adjusted R-squared:  0.9336 
F-statistic:  64.3 on 2 and 7 DF,  p-value: 3.126e-05

(3)同じ地区で広さ=70平米, 築年数=10年, 価格=5.8千万円の提示は妥当か

係数を使って線形式に与えられたデータを代入し価格の予測値を出しても良い。

> coef(d.lm)
(Intercept)      hirosa        tiku 
 1.02012955  0.06680477 -0.08082993 

> sum(coef(d.lm) * c(1,70,10) )
[1] 4.888164

が、predict関数を用いてみると、

# 新しいデータをデータフレームで用意し、
givenData <- data.frame(hirosa=70,tiku=10)

> # 予測区間を出す
> predict(d.lm,newdata=givenData,interval = "predict")
       fit      lwr      upr
1 4.888164 4.214119 5.562209

と、予測値と予測区間が出るので便利。参考書と値が一致していることが確認できた。

2019年6月 統計検定準一級 問1

復習

はじめに

本番で解けなかった問題を解いてみます。今回は問１です。この問題で問われていることは

  • 確率分布の和
  • 条件付き確率分布

です。似たような問題ないかなぁと調べてみるとなんと、アクチュアリーの昭和39年数学1の問３にほぼ同じような問題があったので、これを見つつ今回の問題を解いてみることにしました。

問題を解く

以下、

  • λ1 : 3
  • λ2: 2
  • Z : 4

を代入すると記述1〜記述4の解となります。

ポアソン分布の性質

ポアソン分布P(X = k ; {\lambda}) = exp(-{\lambda}) \Big( \frac{ {\lambda}^k }{k!} \Big) は、

  • 平均 : λ
  • 分散 : λ

です。

ポアソン分布に従う確率変数の和の分布

P(X = k ; \lambda_1), P(Y = k ; {\lambda}_2)の時、P(X + Y = Z )が従う分布を求めます。

(はてなのmathjax記法がエラるので画像にて。。)

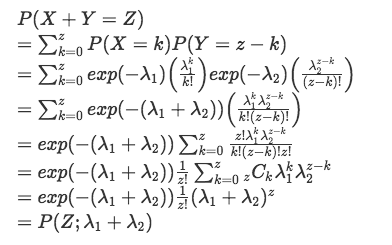
となるので、

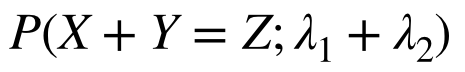
が和の分布となる(ポアソン分布の再生性が確認できた)。よって、和の分布は

  • 平均 : λ1 + λ2
  • 分散 : λ1 + λ2

となる。

条件付き確率分布

求めるのは、

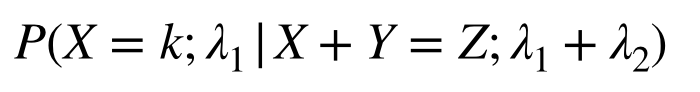
という確率分布である。計算すると、

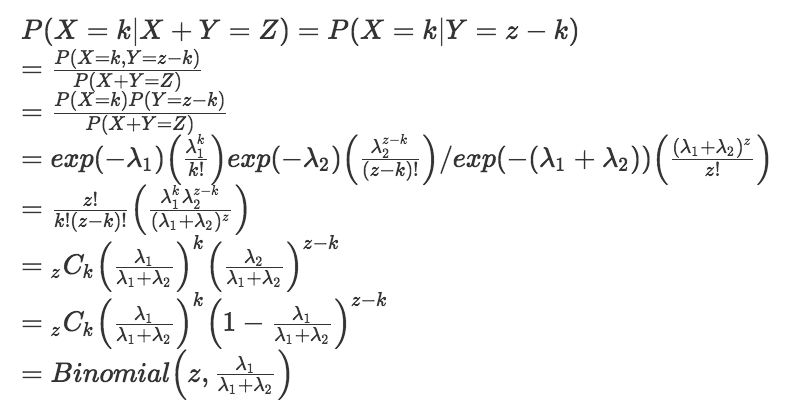
となるので、この条件付き確率分布は二項分布となる。

したがって、平均値は

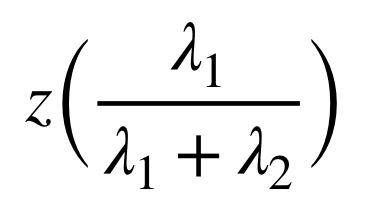
となる。

axjack is said to be an abbreviation for An eXistent JApanese Cool Klutz.