2019-12-23

『確率４万分の１、県の入札くじに６回連続当選「奇跡的」』なのかどうかを調べよう

R 調べ物統計

www.asahi.com

動機

面白いニュースを見かけたので計算してみましたなポストです。記事のこの部分に注目しました。

６回のくじにはそれぞれ制限価格で入札した３～８の鑑定業者が参加した。６回連続で当たる確率を計算すると約４万分の１となる。

奇跡ってどのくらいの割合で起きるのかな？もうすぐクリスマスだしってことでRでやってみます。

まず引用箇所を表にすると、

i回目	鑑定業者数 X_i
1	X_1
2	X_2
3	X_3
4	X_4
5	X_5
6	X_6

ここでX_i ∈ [3,8]の整数で、「６回連続で当たる確率を計算すると約４万分の１」を満たすX_iであって欲しいってことでX_iを全部掛け算したら4万になれば良いでしょう。

とりあえずそのような鑑定業者数の組み合わせを力技で探すと、

kgyousya <- c(3,4,5,6,7,8)

kaisuu <- data.frame(
  x1=kgyousya
  ,x2=kgyousya
  ,x3=kgyousya
  ,x4=kgyousya
  ,x5=kgyousya
  ,x6=kgyousya
)

kaisuu.d <- expand.grid(kaisuu)
kaisuu.m <- as.matrix(kaisuu.d)

kaisuu.prod <- apply(kaisuu.m,MARGIN = 1,prod)

table( kaisuu.prod[(kaisuu.prod > 39000) & (kaisuu.prod < 41000)] )

#> table( kaisuu.prod[(kaisuu.prod > 39000) & (kaisuu.prod < 41000)] )
#
#39200 40000 40320 40960 
#180    15   720    60

915ケースありました。

次に、掛け算して39,200〜40,960となるような鑑定業者数の組み合わせ：915ケースで、各ケースを10000回シミュレーションする。そして各ケースで確率4万分の1以下が10000回中何回起きるかを調べる。(←奇跡の割合）最後に奇跡の割合の分布を観察しましょう。

# 候補のケース数: 915
#> nrow(kaisuu.sub)
#[1] 915
mycase <- nrow(kaisuu.sub)
results <- numeric(mycase)

# シミュレーション回数
ntimes <- 1:10000
result <- numeric( length(ntimes) )

for(j in 1:mycase){
  for(i in ntimes){
    np <- sample(c(0,1),size=6,replace = TRUE, prob=c(.5,.5))
    result[i] <- prod( abs( np  -  (1/kaisuu.sub[j,]) ) )
  }
  results[j] <- sum( result < 1/40000 )/length(result)
}

結果

度数分布表

> table(results)
results
    0 0.005 0.006 0.007 0.008 0.009  0.01 0.011 0.012 0.013 0.014 0.015 0.016 0.017 0.018 
  180     1     3     7     8    17    21    56    63    66    64    54    74    74    49 
0.019  0.02 0.021 0.022 0.023 0.024 0.025 0.026 0.027 0.028 0.029 
   46    45    30    18    19     7     4     4     3     1     1

要約値

> summary(results)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
0.00000 0.01000 0.01400 0.01223 0.01700 0.02900

どんなケースでも平均すれば1%ぐらいは起きるのでは？という見方で良いのかなぁ・・・。

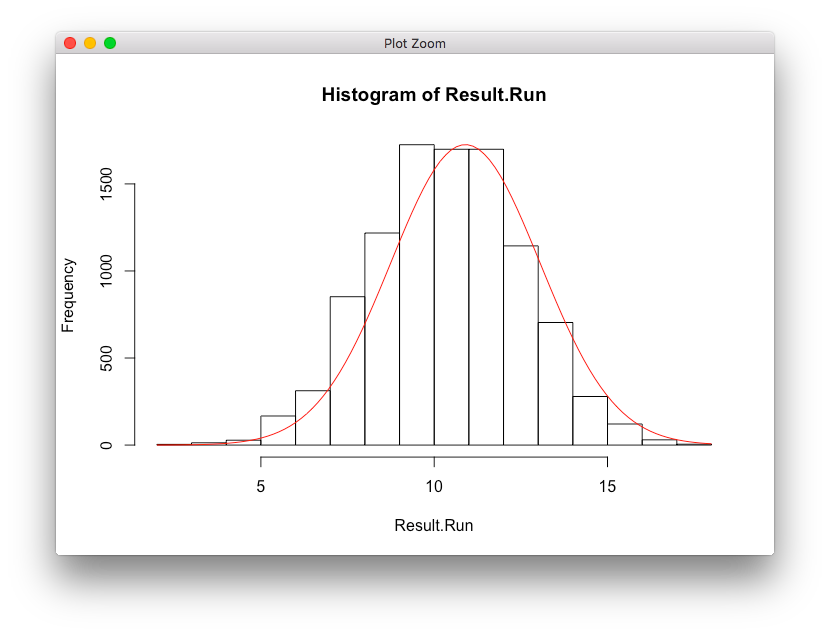
プロット

f:id:axjack:20191223212612p:plain

f:id:axjack:20191223212627p:plain

感想

こういうの式だけ立てて計算できるようになりたいですなぁ。

2019-11-19

2018年11月統計検定2級問9

勉強復習

この問題をなぜ解くのか
問題文の概要
解答
- 問(1)
- 問(2)

この問題をなぜ解くのか

前にこんなこと

統計検定であって確率検定ではないので、サイコロを７回投げる時２以下の目が出る確率を解けるようになってもなんだかなぁ
統計検定２級に合格したので勉強法やら参考書などを書いておきます。 - axjack's blog

を書きました。がしかし、統計検定準1級の勉強をしていく中「やっぱ確率もちゃんと解けないとダメじゃん😢」と気持ちが一転したので改めてちゃんと解いてみようと思った次第です。

問題文の概要

どの面も等確率で出る6面のサイコロを7回投げる。2以下の目が出る回数をXとする。

問(1)：P(X = x+1)とP(X = x)の比、i.e. $\frac{ P(X=x+1) }{ P(X=x) }$ を求めよ
問(2)：P(X = x) が最大となるxは?

解答

問(1)

$\displaystyle X_i$ を出目が2以下の時に1、そうでない時を0とすると $\displaystyle X_i$ はベルヌーイ分布：Bin(1,p)に従う。ここでp=1/3である。この時、 $\displaystyle X = \sum X_i$ は二項分布：Bin(n,p)に従う。よって、確率質量関数は $\displaystyle P(X=k)= {}_n \mathrm{ C }_k p^{k} (1-p)^{n-k}$ となる。ここで、n=7, p=1/3を代入するとP(X=x)とP(X=x+1)はそれぞれ、

$\displaystyle P(X=x) = {}_7 \mathrm{ C }_x (1/3)^x (2/3)^{7-x}$
$\displaystyle P(X=x+1) = {}_7 \mathrm{ C }_{x+1} (1/3)^{x+1} (2/3)^{7-(x+1)}$

となる。すると、

$\displaystyle \frac{P(X=x+1)}{P(X=x)} \\ \displaystyle = \frac{ {}_7 \mathrm{ C }_{x+1} (1/3)^{x+1} (2/3)^{7-(x+1)} } { {}_7 \mathrm{ C }_x (1/3)^x (2/3)^{7-x} } \\ \displaystyle = \frac{ {}_7 \mathrm{ C }_{x+1} (1/3)^{x} (1/3) (2/3)^{7-x} (2/3)^{-1} } { {}_7 \mathrm{ C }_x (1/3)^x (2/3)^{7-x} } \\ \displaystyle = \frac{ \frac{ 7! }{ (7-(x+1))! (x+1)! } (1/3)^{x} (1/3) (2/3)^{7-x} (2/3)^{-1} }{ \frac{7!}{(7-x)!x!} (1/3)^x (2/3)^{7-x} }\\ \displaystyle = \frac{ \frac{ 7! }{ (6-x)! (x+1)x! } (1/3)^{x} (1/3) (2/3)^{7-x} (2/3)^{-1} }{ \frac{7!}{(7-x)(6-x)!x!} (1/3)^x (2/3)^{7-x} } \\ \displaystyle = \frac { \frac{ 1 }{ x+1 } (1/3) (3/2) }{ \frac{1}{7-x} } = \frac{ 7-x }{ 2x+2 }$

となる。よって、 $\displaystyle \frac{P(X=x+1)}{P(X=x)} = \frac{ 7-x }{ 2x+2 }$

問(2)

P(X=x)が最大となるxを $\displaystyle \frac{P(X=x+1)}{P(X=x)} = \frac{ 7-x }{ 2x+2 } = Q(x)$ を用いて考えてみると、Q(x)が1より大であればP(X=x+1) > P(x)であると言えるし1未満であればP(X=x+1) < P(x)と言える。具体的にxへ0から6を代入すると、

x	Q(x)	判定
0	7/2 > 1	P(1) > P(0)
1	6/4 > 1	P(2) > P(1)
2	5/6 < 1	P(3) < P(2)
3	4/8 < 1	P(4) < P(3)
4	3/10 < 1	P(5) < P(4)
5	2/12 < 1	P(6) < P(5)
6	1/14 < 1	P(7) < P(6)

となる。関数の増減表のように判定の列を眺めれば、P(x)はP(2)がピークであることからP(X = x) が最大となるxは2である。

2019-11-04

超幾何分布

統計勉強復習 R

何度やっても忘れるのでブログに書いて覚えよう。

超幾何分布の確率質量関数

$\displaystyle P(X=x) = f(x; N,M,n) = \frac{ \binom{M}{x} \binom{N-M}{n-x} } { \binom{N}{n} }$

計算例

その1

男50人女50人から10人を選ぶ。10人のうち男3人女7人となる確率pは、超幾何分布を用いて

$\displaystyle p = \frac{ \binom{50}{3} \binom{50}{7} }{ \binom{100}{10}}$

その2

統計検定準一級2017年問10より引用。表の80人から30人を無作為抽出する。その30人のうち男性かつ就職している人数Xは超幾何分布に従う。

＼	就職	非就職	計
男性	38	3	41
女性	30	9	39
計	68	12	80

80人から30人を選ぶ
「男性かつ就職」である人：38
「男性かつ就職」でない人：80-38 = 42

と整理して、
$\displaystyle P(X=x) = \frac{ \binom{38}{x} \binom{42}{30-x} }{ \binom{80}{30} }$

となる。

その3

同じ表を用いて、80人から20人を無作為抽出する。その20人のうち「女性かつ非就職」な人数Xは超幾何分布に従う。

80人から20人を選ぶ
「女性かつ非就職」である人：9
「女性かつ非就職」でない人：80-9 = 71

と整理して、
$\displaystyle P(X=x) = \frac{ \binom{9}{x} \binom{71}{20-x} }{ \binom{80}{20} }$

となる。

Rで計算する

choose関数で立てた式が超幾何分布の質量関数dhyperと同じことを確認。

# その1
> choose(50,3)*choose(50,7)/choose(100,10)
[1] 0.1130964
> dhyper(3,50,50,10)
[1] 0.1130964

dhpyer(x,m,n,k)の引数*1は、

x: vector of quantiles representing the number of white balls drawn without replacement from an urn which contains both black and white balls.
m: the number of white balls in the urn.
n: the number of black balls in the urn.
k:the number of balls drawn from the urn.

*1:https://www.rdocumentation.org/packages/stats/versions/3.6.1/topics/Hypergeometric

2019-09-26

連の検定(Runs Test for Detecting Non-randomness)

統計調べ物 R

はじめに

連の検定についてよく分からなかったのでRで実装して確かめてみました。

連とは？

２値{A,B}を取る系列ABAABBAAABBBABがあった時、これをA | B | AA | BB | AAA | BBB | A | Bと連続する同じ値ごとに分割できるように見える。この時同じ文字または記号のひと続きを連(run)*1と言い、またひと続きの個数を連の長さ*2と言う。この場合、Aの連が4つ(= {A,AA,AAA,A})とBの連が4つ(= {B,BB,BBB,B})あることが分かる。AAAAAAAAABBBBBBBBBBBであれば、Aの連が1つでBの連が1つとなる。

確かめたこと

Aの数(= Na)とBの数(= Nb)が与えられた時、N = Na+Nbの大きさを持つ系列は、

もしA・Bがランダムに現れるなら(←帰無仮説)連の数はどのような分布になるのか　→　正規分布
連の数の平均値・分散が以下の式*3どおりとなるか

f:id:axjack:20190926230103p:plain

を確かめた。

ソース

# 連の検定####
rm(list=ls())

# --------------------
# 関数: generateRun ####
# --------------------
# 引数
#   Na_: Aの個数
#   Nb_: Bの個数
# 戻り値
#   連の数を返す関数
# --------------------
generateRun <- function(Na_, Nb_){
  return(
      function(dummy){
        N <- Na_ + Nb_
        Arep <- rep(TRUE,Na_)
        Brep <- rep(FALSE,Nb_)
        AB <- c(Arep,Brep)
        xx <- sample(AB, N, replace = FALSE)
        yy <- xx[1:(N-1)]
        zz <- xx[2:N]
        return( sum( yy != zz)  + 1 )
    }
  )
}

# シミュレーション ####
## 各種変数設定
Na <- 9 # Aの個数
Nb <- 11 # Bの個数
sim_N <- 10000 # シミュレーション回数

## 平均値と分散
( t_mean <- (2*Na*Nb)/(Na+Nb) + 1 ) # 平均値
( t_var <- (2*Na*Nb*(2*Na*Nb - Na - Nb))/((Na+Nb)^2 * (Na+Nb-1)) ) # 分散

# シミュレーション実行
Result.Run <- sapply( 1:sim_N, generateRun(Na,Nb) )

# 要約
table(Result.Run)
summary( Result.Run )
var( Result.Run )

# グラフ表示
hist(Result.Run,breaks = seq(min(Result.Run),max(Result.Run),1))
par(new=T)

# 正規分布を重ね合わせ
curve(dnorm(x,t_mean,sqrt(t_var)),min(Result.Run),max(Result.Run),xlab="",ylab="",xaxt="n", yaxt="n",col="red",bty="n")

結果の確認

数値の確認

> # シミュレーション ####
> ## 各種変数設定
> Na <- 9 # Aの個数
> Nb <- 11 # Bの個数
> sim_N <- 10000 # シミュレーション回数
> ## 平均値と分散
> ( t_mean <- (2*Na*Nb)/(Na+Nb) + 1 ) # 平均値
[1] 10.9
> ( t_var <- (2*Na*Nb*(2*Na*Nb - Na - Nb))/((Na+Nb)^2 * (Na+Nb-1)) ) # 分散
[1] 4.637368
> # シミュレーション実行
> Result.Run <- sapply( 1:sim_N, generateRun(Na,Nb) )
> # 要約
> table(Result.Run)
Result.Run
   2    3    4    5    6    7    8    9   10   11   12   13   14   15   16   17   18 
   1    3   13   28  167  312  852 1218 1725 1699 1699 1144  704  279  121   30    5 
> summary( Result.Run )
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   2.00    9.00   11.00   10.89   12.00   18.00 
> var( Result.Run )
[1] 4.666794

プロット

f:id:axjack:20190926230756p:plain

結果の考察

計算した平均値・分散がシミュレーションの結果とだいたい合っていることがわかった。
ヒストグラムとカーブプロットが大まかにあっている。

おわりに

帰無仮説の下での平均値・分散の式が奇妙で覚えられないし式を見てもあまり実感が湧かなかったものの、シミュレーションしてみると確かに平均値・分散がそれっぽく合うのでこの式の妥当性を確認することができた。疑わしい系列があってもこれで確かめることができそうだ。

参考

連の検定関連

R言語のplot関連

49. 図の重ね合わせ
- 図の重ね合わせ方法を参考にしました。
正規分布のグラフをRで描く。【curve()の使い方】
- 正規分布をcurveで書く方法を参考にしました。
R 使い方軸・ラベルの調整（向き・サイズ・色など）グラフの描き方
- plotを重ねる時に軸やラベルを消す方法を参考にしました。

*1:[連の検定]より引用

*2:[連の検定]より引用

*3:式は[連の検定]より引用

2019-09-12

自由度調整済み決定係数を決定係数で表す

統計復習

やること

タイトルの通り式変形をするだけです。

式変形

$\displaystyle R_{adj}^2 = 1 - \frac{ \frac{\sum{(y_i - \hat{y_{i}})^2}}{n-k-1} }{ \frac{\sum{(y_i - \bar{y})^2 }}{n-1} } \\ \displaystyle = 1 - \frac{n-1}{n-k-1} \frac{ \sum{(y_i - \hat{y_{i}})^2}} {\sum{ (y_i - \bar{y} )^2 } } \\ \displaystyle = \frac{n-1}{n-k-1}\Bigl( \frac{n-k-1}{n-1} - \frac{ \sum{(y_i - \hat{y_{i}})^2}} {\sum{ (y_i - \bar{y} )^2 } } \Bigr) \\ \displaystyle = \frac{n-1}{n-k-1}\Bigl( \frac{n-k-1}{n-1} + \Bigl(1 - \frac{ \sum{(y_i - \hat{y_{i}})^2}} {\sum{ (y_i - \bar{y} )^2 } } \Bigr) - 1 \Bigr) \\ \displaystyle = \frac{n-1}{n-k-1}\Bigl( \frac{n-k-1}{n-1} + R^2 - 1 \Bigr) \\ \displaystyle = \frac{n-1}{n-k-1}\Bigl( R^2 - \frac{k}{n-1} \Bigr) \\$

2019-09-04

2019年8月をワールドワイドに考える

メモプログラミング調べ物

はじめに

UTCを考慮すると途端にわけわからなくなったので整理する。

UTCとは

wikiで協定世界時 - Wikipediaをみませう。

UTCってプラマイいくつまであるの？

時間帯 (標準時) - WikipediaによるとからUTC-12からUTC+14まである。日本はUTC+9

2019年8月をUTCで列挙する

以下の時間帯で考える。

UTC-12
UTC0
UTC+9
UTC+14

すると次の表のようになる

UTC-12	UTC0	UTC+9	UTC+14
7/30 22:00	7/31 10:00	7/31 19:00	8/01 00:00
7/31 03:00	7/31 15:00	8/01 00:00	8/01 05:00
7/31 03:00	8/01 00:00	8/01 09:00	8/01 14:00
8/01 00:00	8/01 12:00	8/01 21:00	8/02 02:00
…	…	…	…
8/30 22:00	8/31 10:00	8/31 19:00	9/01 00:00
8/31 03:00	8/31 15:00	9/01 00:00	9/01 05:00
8/31 03:00	9/01 00:00	9/01 09:00	9/01 14:00
9/01 00:00	9/01 12:00	9/01 21:00	9/02 02:00

結局2019年8月とは

UTC+14が世界で最も早く8/1を迎えるので、UTC0で考えれば7/31 10:00(⇔日本時間 7/31 19:00)
UTC-12が世界で最も遅く9/1を迎えるので、UTC0で考えれば9/1 12:00(⇔日本時間 9/1 21:00)

の時間帯を抽出すればとりあえず取りこぼすことはなさそうだ。

参考

タイムゾーンを考慮した日時の扱いのベストプラクティス - エムスリーテックブログ

2019-08-25

久保川『現代数理統計学の基礎』p.25 命題2.21 (平方変換)

統計確率

やること

確率変数 $X$ の確率密度関数を $f_X(x)$ とする。 Xの平方変換 $Y=X^2$ に対して、Yの密度関数は？
という命題について、式変形の行間を埋めます。

以下途中式

$y >0$ に対して $\{x|x^2 \le y\} = \{x|-\sqrt{y} \le x \le \sqrt{y} \}$ であるから

$\displaystyle f_Y (y) = \frac{d}{dy} P( X \in \{ x|x^2 \le y\} ) \\\\ \displaystyle = \frac{d}{dy} \int_{-\sqrt{y}}^{\sqrt{y}} f_X (x) dx \\\\ \displaystyle = \frac{d}{dy} \Bigl( F_X(\sqrt{y}) - F_X(-\sqrt{y}) \Bigr) \\\\ \displaystyle = f_X(\sqrt{y})\frac{d}{dy}(\sqrt{y}) - f_X(-\sqrt{y})\frac{d}{dy}(-\sqrt{y}) \\\\ \displaystyle = f_X(\sqrt{y})\frac{1}{2\sqrt{y}} - f_X(-\sqrt{y})\frac{-1}{2\sqrt{y}} \\\\ \displaystyle = f_X(\sqrt{y})\frac{1}{2\sqrt{y}} + f_X(-\sqrt{y})\frac{1}{2\sqrt{y}} \\\\ \displaystyle = \Bigl( f_X(\sqrt{y}) + f_X(-\sqrt{y}) \Bigr)\frac{1}{2\sqrt{y}}$

と無事式変形できる。

2019-08-14

多変量解析法入門pp.52-53のテコ比の式変形

統計勉強

やること

多変量解析法入門p.52の式(4.35)あたりの式変形の行間を埋めてみる。

式変形

式(4.35)にて
$\begin{eqnarray} \hat{y_k} &=& \hat{\beta_0} + \hat{\beta_1}x_k \\ &=& \bar{y} + \hat{\beta_1}(x_k - \bar{x} ) \\ &=& \frac{\Sigma y_i}{n} + \frac{ (x_k - \bar{x}) \Sigma(x_i-\bar{x})y_i }{ S_{xx} } \end{eqnarray}$

ここで、上式の第一項は

$\displaystyle \frac{\Sigma y_i}{n} = \frac{1}{n}y_1 + \frac{1}{n}y_2 + \cdots + \frac{1}{n}y_k + \cdots + \frac{1}{n}y_n \\ \displaystyle = \begin{bmatrix} y_1 & y_2 & \cdots & y_k & \cdots & y_n \end{bmatrix} \begin{bmatrix} \frac{1}{n} & \frac{1}{n} & \cdots & \frac{1}{n} \end{bmatrix}'$

第二項は

$\displaystyle \frac{ (x_k - \bar{x}) \Sigma(x_i-\bar{x})y_i }{ S_{xx} } = \Bigl( \frac{(x_k - \bar{x} )}{S_{xx}} \Bigr) \Bigl( (x_1-\bar{x})y_1 + (x_2-\bar{x})y_2 + \cdots + (x_n-\bar{x})y_n \Bigr) \\ \displaystyle = \begin{bmatrix} y_1 & y_2 & \cdots & y_k & \cdots & y_n \end{bmatrix} \begin{bmatrix} \Bigl( \frac{(x_k-\bar{x})(x_1 - \bar{x})}{S_{xx}} \Bigr) & \Bigl( \frac{(x_k-\bar{x})(x_2 - \bar{x})}{S_{xx}} \Bigr) & \cdots & \Bigl( \frac{(x_k-\bar{x})(x_k - \bar{x})}{S_{xx}} \Bigr) & \cdots & \Bigl( \frac{(x_k-\bar{x})(x_n - \bar{x})}{S_{xx}} \Bigr) \end{bmatrix}'$

より、バラバラにした項を足して元に戻せば、

$\displaystyle \hat{y_k} = \begin{bmatrix} y_1 & \cdots & y_k & \cdots & y_n \end{bmatrix} \begin{bmatrix} \Bigl( \frac{1}{n} + \frac{(x_k-\bar{x})(x_1 - \bar{x})}{S_{xx}} \Bigr) & \cdots & \Bigl( \frac{1}{n} + \frac{(x_k-\bar{x})(x_k - \bar{x})}{S_{xx}} \Bigr) & \cdots & \Bigl( \frac{1}{n} + \frac{(x_k-\bar{x})(x_n - \bar{x})}{S_{xx}} \Bigr) \end{bmatrix}' \\ \displaystyle \iff \hat{y_k} = \begin{bmatrix} y_1 & \cdots & y_k &\cdots& y_n\end{bmatrix} \begin{bmatrix} h_{k1} & \cdots & h_{kk} & \cdots & h_{kn} \end{bmatrix}'$

となる。

ということで、 $y_k$ の係数

$\displaystyle h_{kk} = \frac{1}{n} + \frac{ (x_k - \bar{x})^2 }{ S_{xx} }$

をテコ比と呼ぶ。式(4.36)